How to Calculate Compound Interest

Finding Annual Compound Interest

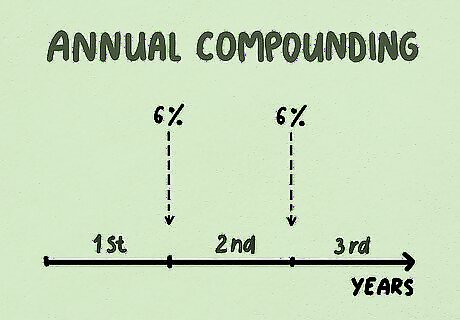
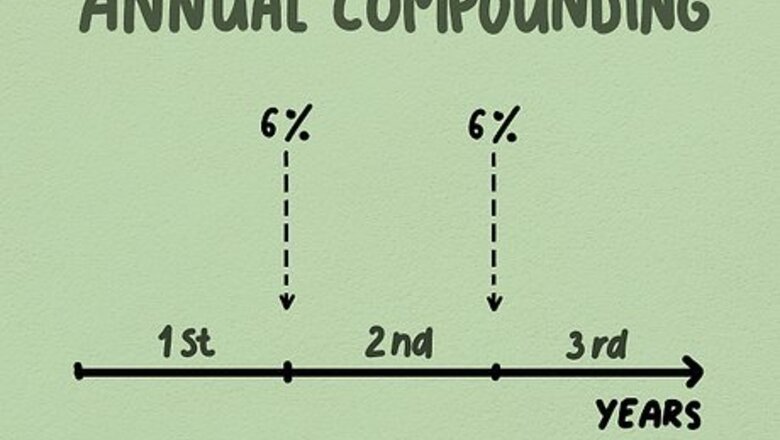
Define annual compounding. The interest rate stated on your investment prospectus or loan agreement is an annual rate. If your car loan, for example, is a 6% loan, you pay 6% interest each year. Compounding once at the end of the year is the easiest calculation for compounding interest. A debt may compound interest annually, monthly, or even daily. The more frequently your debt compounds, the faster you will accumulate interest. You can look at compound interest from the investor or the debtor’s point of view. Frequent compounding means that the investor’s interest earnings will increase at a faster rate. It also means that the debtor will owe more interest while the debt is outstanding. For example, a savings account may be compounded annually, while a pay-day loan can be compounded monthly or even weekly.

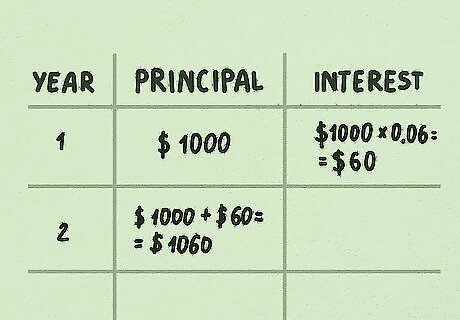
Calculate interest compounding annually for year one. Assume that you own a $1,000, 6% savings bond issued by the US Treasury. Treasury savings bonds pay out interest each year based on their interest rate and current value. Interest paid in year 1 would be $60 ($1,000 multiplied by 6% = $60). To calculate interest for the second year, you need to add the original principal amount to all interest earned to date. In this case, the principal for year 2 would be ($1,000 + $60 = $1,060). The value of the bond is now $1,060 and the interest payment will be calculated from this value.

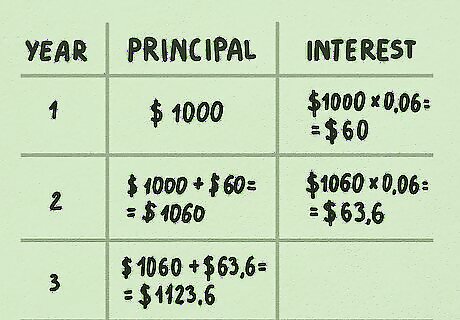
Compute interest compounding for later years. To see the bigger impact of compound interest, compute interest for later years. As you move from year to year, the principal amount continues to grow. Multiply the year 2 principal amount by the bond’s interest rate. ($1,060 X 6% = $63.60). The interest earned is higher by $3.60 ($63.60 - $60.00). That’s because the principal amount increased from $1,000 to $1,060. For year 3, the principal amount is ($1,060 + $63.60 = $1,123.60). The interest earned in year 3 is $67.42. That amount is added to the principal balance for the year 4 calculation. The longer a debt is outstanding, the bigger the impact of compounding interest. Outstanding means that the debt is still owed by the debtor. Without compounding, the year 2 interest would simply be ($1,000 X 6% = $60). In fact, every year’s interest earned would be $60 if you did earn compound interest. This is known as simple interest.

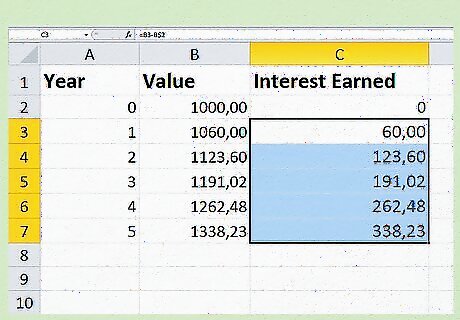
Create an Excel document to compute compound interest. It can be handy to visualize compound interest by creating a simple model in Excel that shows the growth of your investment. Start by opening a document and labeling the top cell in columns A, B, and C "Year," "Value," and "Interest Earned," respectively. Enter the years (0-5) in cells A2 to A7. Enter your principal in cell B2. For example, imagine you are started with $1,000. Input 1000. In cell B3, type "=B2*1.06" and press enter. This means that your interest is being compounded annually at 6% (0.06). Click on the lower right corner of cell B3 and drag the formula down to cell B7. The numbers will fill in appropriately. Place a 0 in cell C2. In cell C3, type "=B3-B$2" and press enter. This should give you the difference between the values in cell B3 and B2, which represents the interest earned. Click on the lower right corner of cell C3 and drag the formula down to cell C7. The values will fill themselves in. Continue this process to replicate the process for as many years as you want to track. You can also easily change values for principal and interest rate by altering the formulas used and cell contents.

Calculating Compound Interest on Investments

Learn the compound interest formula. The compound interest formula solves for the future value of the investment after set number of years. The formula itself is as follows: F V = P ( 1 + i c ) n ∗ c {\displaystyle FV=P(1+{\frac {i}{c}})^{n*c}} FV=P(1+{\frac {i}{c}})^{{n*c}} The variables within the equation are defined as follows:Alternative: For a quick and easy method of calculating compound interest, use the continuous compounding formula. This formula allows you to calculate the maximum future value of your investment based on a theoretically infinite number of compounding periods within a given length of time. To calculate continuous interest, use the formula F V = P V ( e i ∗ t ) {\displaystyle FV=PV(e^{i*t})} {\displaystyle FV=PV(e^{i*t})}, where FV is the future value of the investment, PV is the present value, e is Euler’s number (the constant 2.71828), i is the interest rate, and t is the time in years. "FV" is the future value. This is the result of the calculation. "P" is your principal. "i" represents the annual interest rate. "c" represents the compounding frequency (how many times the interest compounds each year). "n" represents the number of years being measured.

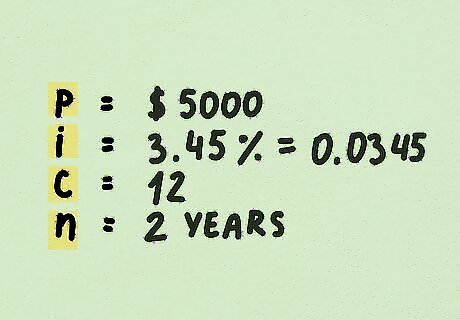
Gather variables the compound interest formula. If interest compounds more often than annually, it is difficult to calculate the formula manually. You can use a compound interest formula for any calculation. To use the formula, you need to gather the following information: Identify the principal of the investment. This is the amount of your initial investment. This could be how much you deposited into the account or the original cost of the bond. For example, imagine your principal in an investment account is $5,000. Locate the interest rate for the debt. The interest rate should be an annual amount, stated as a percentage of the principal. For example, a 3.45% interest rate on the $5,000 principal value. In the calculation, the interest rate will have to be input as decimal. Convert it by dividing the interest rate by 100. In this example, this would be 3.45%/100 = 0.0345. You also need to know how often the debt compounds. Typically, interest compounds annually, monthly, or daily. For example, imagine that it compounds monthly. This means your compounding frequency ("c") would be input as 12. Determine the length of time you want to measure. This could be a goal year for growth, like 5 or 10 years, or this maturity of a bond. The maturity date of a bond is the date that the principal amount of the debt is to be repaid. For the example, we use 2 years, so input 2.

Use the formula. Input your variables in the right places. Check again to make sure that you are inputting them correctly. Specifically, make sure that your interest rate is in decimal form and that you have used the right number for "c" (compounding frequency). The example investment would be input as follows: F V = $ 5000 ( 1 + 0.0345 12 ) 2 ∗ 12 {\displaystyle FV=\$5000(1+{\frac {0.0345}{12}})^{2*12}} FV=\$5000(1+{\frac {0.0345}{12}})^{{2*12}} Compute the exponent portion and the portion of the formula in parenthesis separately. This is a math concept called order of operations. You can learn more about the concept using this link: Apply the Order of Operations.

Finish the math computations in the formula. Simplify the problem by solving for the parts of the equation in parenthesis first, beginning with the fraction. Divide the fraction within parentheses first. The result should be: F V = $ 5000 ( 1 + 0.00288 ) 2 ∗ 12 {\displaystyle FV=\$5000(1+0.00288)^{2*12}} FV=\$5000(1+0.00288)^{{2*12}} Add the numbers within parentheses. The result should be: F V = $ 5000 ( 1.00288 ) 2 ∗ 12 {\displaystyle FV=\$5000(1.00288)^{2*12}} FV=\$5000(1.00288)^{{2*12}} Solve the multiplication within the exponent (the last part above the closing parenthesis). The result should look like this: F V = $ 5000 ( 1.00288 ) 24 {\displaystyle FV=\$5000(1.00288)^{24}} FV=\$5000(1.00288)^{{24}} Raise the number within the parentheses to the power of the exponent. This can be done on a calculator by entering the value in parentheses (1.00288 in the example) first, pressing the x y {\displaystyle x^{y}} x^{y} button, then entering the exponent (24 in this case) and pressing enter. The result in the example is F V = $ 5000 ( 1.0715 ) {\displaystyle FV=\$5000(1.0715)} FV=\$5000(1.0715) Finally, multiply the principal by the number in parentheses. The result in the example is $5,000*1.0715, or $5,357.50. This is the value of the account at the end of the 2 years.

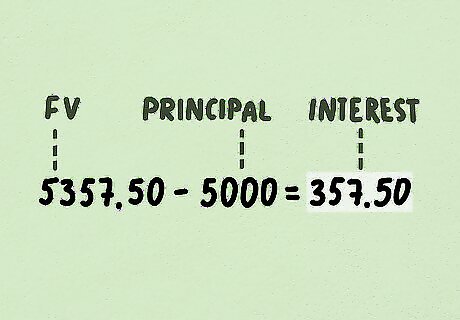
Subtract the principal from your answer. This will give you the amount of interest earned. Subtract the principal of $5,000 from the future value of $5357.50 to get $5,357.50-$5,000, or $357.50 You will earn $357.50 in interest over the 2 years.

Calculating Compound Interest with Regular Payments

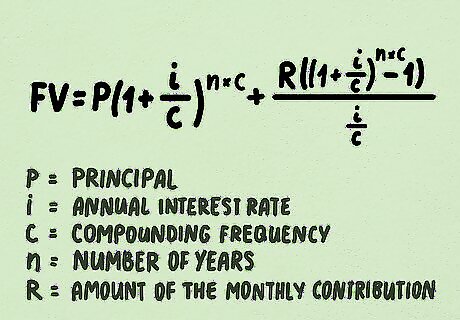
Learn the formula. Compounding interest accounts can increase even faster if you make regular contributions to them, such as adding a monthly amount to a savings account. The formula is longer than that used to calculate compound interest without regular payments, but follows the same principles. The formula is as follows: F V = P ( 1 + i c ) n ∗ c + R ( ( 1 + i c ) n ∗ c − 1 ) i c {\displaystyle FV=P(1+{\frac {i}{c}})^{n*c}+{\frac {R((1+{\frac {i}{c}})^{n*c}-1)}{\frac {i}{c}}}} FV=P(1+{\frac {i}{c}})^{{n*c}}+{\frac {R((1+{\frac {i}{c}})^{{n*c}}-1)}{{\frac {i}{c}}}}The variables within the equation are also the same as the previous equation, with one addition: "P" is the principal. "i" is the annual interest rate. "c" is the compounding frequency and represents how many times the interest is compounded each year. "n" is the number of years. "R" is the amount of the monthly contribution.

Compile the necessary variables. To compute the future value of this type of account, you will need the principal (or present value) of the account, the annual interest rate, the compounding frequency, the number of years being measured, and the amount of your monthly contribution. This information should be in your investment agreement. Be sure to convert the annual interest rate into a decimal. Do this by dividing the rate by 100. For example, using the above 3.45% interest rate, we would divide 3.45 by 100 to get 0.0345. Some accounts compound multiple times per year. For example, your account may have monthly compounding instead of annual. For compounding frequency, simply use the number of times per year that the interest compounds. This means annually is 1, quarterly is 4, monthly is 12, and daily is 365 (don't worry about leap years).

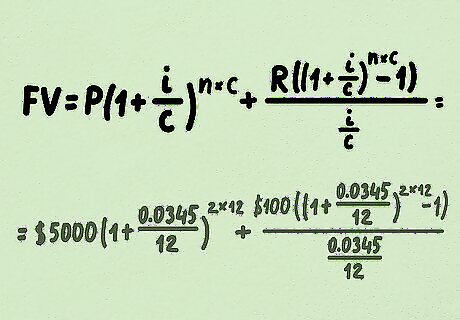
Input your variables. Continuing with the example from above, imagine that you decide to also contribute $100 per month to your account. This account, with a principal value of $5,000, compounds monthly and earns 3.45% annual interest. We will measure the growth of the account over two years. The completed formula using this information is as follows: F V = $ 5 , 000 ( 1 + 0.0345 12 ) 2 ∗ 12 + $ 100 ( ( 1 + 0.0345 12 ) 2 ∗ 12 − 1 ) 0.0345 12 {\displaystyle FV=\$5,000(1+{\frac {0.0345}{12}})^{2*12}+{\frac {\$100((1+{\frac {0.0345}{12}})^{2*12}-1)}{\frac {0.0345}{12}}}} FV=\$5,000(1+{\frac {0.0345}{12}})^{{2*12}}+{\frac {\$100((1+{\frac {0.0345}{12}})^{{2*12}}-1)}{{\frac {0.0345}{12}}}}

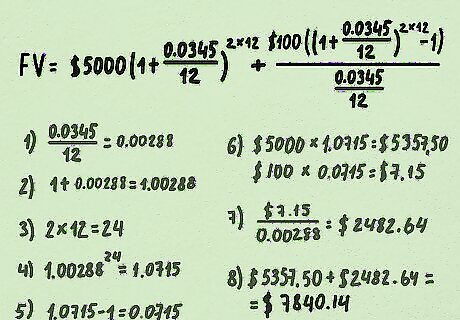
Solve the equation. Again, remember to use the proper order of operations to do so. This means that you start by calculating the values inside of parentheses. Solve for the fractions with parentheses first. This means dividing "i" by "c" in three places, all for the same result of 0.00288. The equation now looks like this: F V = $ 5 , 000 ( 1 + 0.00288 ) 2 ∗ 12 + $ 100 ( ( 1 + 0.00288 ) 2 ∗ 12 − 1 ) 0.00288 {\displaystyle FV=\$5,000(1+0.00288)^{2*12}+{\frac {\$100((1+0.00288)^{2*12}-1)}{0.00288}}} FV=\$5,000(1+0.00288)^{{2*12}}+{\frac {\$100((1+0.00288)^{{2*12}}-1)}{0.00288}} Solve the addition within the parentheses. This means adding the 1 to the result from the last part. This gives: F V = $ 5 , 000 ( 1.00288 ) 2 ∗ 12 + $ 100 ( ( 1.00288 ) 2 ∗ 12 − 1 ) 0.00288 {\displaystyle FV=\$5,000(1.00288)^{2*12}+{\frac {\$100((1.00288)^{2*12}-1)}{0.00288}}} FV=\$5,000(1.00288)^{{2*12}}+{\frac {\$100((1.00288)^{{2*12}}-1)}{0.00288}} Solve the multiplication within the exponents. This means multiplying the 2 numbers that are smaller and above the closing parentheses. In the example, this is 2*12 for a result of 24. This gives: F V = $ 5 , 000 ( 1.00288 ) 24 + $ 100 ( ( 1.00288 ) 24 − 1 ) 0.00288 {\displaystyle FV=\$5,000(1.00288)^{24}+{\frac {\$100((1.00288)^{24}-1)}{0.00288}}} FV=\$5,000(1.00288)^{{24}}+{\frac {\$100((1.00288)^{{24}}-1)}{0.00288}} Solve the exponents. This means raising the amount within parentheses to the result of the last step. On a calculator, this is done by entering the value in parentheses (1.00288 in the example), pressing the x y {\displaystyle x^{y}} x^{y} key, and then entering the exponent value (which is 24 here). This gives: F V = $ 5 , 000 ( 1.0715 ) + $ 100 ( 1.0715 − 1 ) 0.00288 {\displaystyle FV=\$5,000(1.0715)+{\frac {\$100(1.0715-1)}{0.00288}}} FV=\$5,000(1.0715)+{\frac {\$100(1.0715-1)}{0.00288}} Subtract. Subtract the 1 from the result of the last step in the right part of the equation (here 1.0715 minus 1). This gives: F V = $ 5 , 000 ( 1.0715 ) + $ 100 ( 0.0715 ) 0.00288 {\displaystyle FV=\$5,000(1.0715)+{\frac {\$100(0.0715)}{0.00288}}} FV=\$5,000(1.0715)+{\frac {\$100(0.0715)}{0.00288}} Multiply. This means multiplying the principal by the number is the first set of parentheses and the monthly contribution by the same number in parentheses. This gives: F V = $ 5 , 357.50 + $ 7.15 0.00288 {\displaystyle FV=\$5,357.50+{\frac {\$7.15}{0.00288}}} FV=\$5,357.50+{\frac {\$7.15}{0.00288}} Divide the fraction. This gives F V = $ 5 , 357.50 + $ 2 , 482.64 {\displaystyle FV=\$5,357.50+\$2,482.64} FV=\$5,357.50+\$2,482.64 Add. Finally, add the 2 numbers to get the future value of the account. This gives $5,357.50 + $2,482.64, or $7,840.14. This is the value of the account after the 2 years.

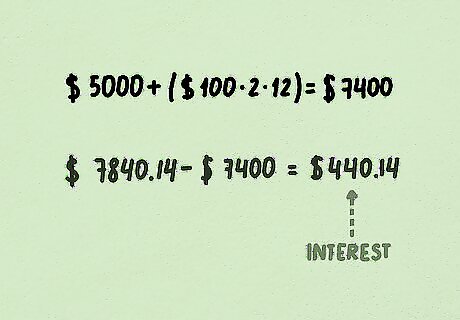
Subtract the principal and payments. To find the interest earned, you have to subtract the amount of money you put into the account. This means adding the principal, $5,000, to the total value of contributions made, which is 24 contributions (2 years* 12 months/year) times the $100 you put in each month for a total of $2,400. The total is $5,000 plus $2,400, or $7,400. Subtracting $7,400 from the future value of $7,840.14, you get the amount of interest earned, which is $440.14.

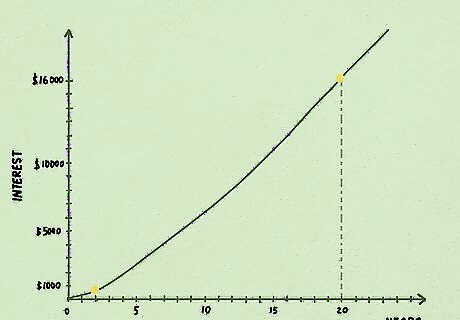
Extend your calculation. To really see the benefit of compound interest, imagine that you continue adding money monthly to the same account for 20 years instead of 2. In this case, your future value would be about $45,000, even though you will have only contributed $29,000, meaning that you will have earned $16,000 in interest.