How to Solve Exponents

Solving Basic Exponents

Learn the correct words and vocabulary for exponent problems. When you have an exponent, like 2 3 {\displaystyle 2^{3}} 2^{3}, you have two simple parts. The bottom number, here a 2, is the base. The number it is raised to, here a 3, is known as the exponent or power. If you are talking about 2 3 {\displaystyle 2^{3}} 2^{3}, you would say it is "two to the third," "two to the third power," or "two raised to the third power." If a number is raised to the second power, like 5 2 {\displaystyle 5^{2}} 5^{2}, you can also say that the number is squared, such as "five squared." If a number is raised to the third power, like 10 3 {\displaystyle 10^{3}} 10^{3}, you can also say it is cubed, such as "ten cubed." If a number has no exponent shown, like a simple 4, it is technically to the first power and can be rewritten as 4 1 {\displaystyle 4^{1}} 4^{1}. If the exponent is 0, and a "non-zero number" is raised to the "zero power", then the whole thing equals 1, such as 4 0 = 1 {\displaystyle 4^{0}=1} 4^{0}=1 or even something like ( 3 / 8 ) 0 = 1. {\displaystyle (3/8)^{0}=1.} (3/8)^{0}=1. There is more about this in the "Tips" section.

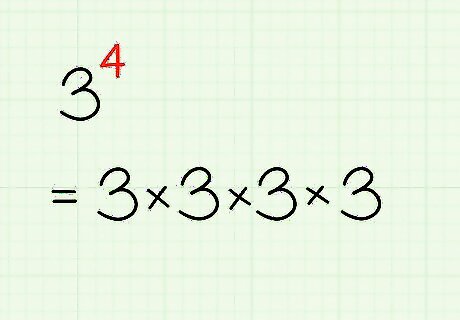
Multiply the base repeatedly for the number of factors represented by the exponent. If you need to solve an exponent by hand, start by rewriting it as a multiplication problem. You want to multiply the base by itself for the number of the exponent. So, if you have 3 4 {\displaystyle 3^{4}} 3^{4} you would multiply three in a series of four separate factors, or 3 ∗ 3 ∗ 3 ∗ 3 {\displaystyle 3*3*3*3} 3*3*3*3. More examples include: 4 5 = 4 ∗ 4 ∗ 4 ∗ 4 ∗ 4 {\displaystyle 4^{5}=4*4*4*4*4} 4^{5}=4*4*4*4*4 8 2 = 8 ∗ 8 {\displaystyle 8^{2}=8*8} 8^{2}=8*8 Ten cubed = 10 ∗ 10 ∗ 10 {\displaystyle =10*10*10} =10*10*10

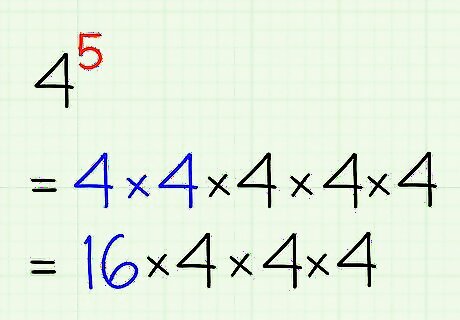
Solve an expression: Multiply the first two numbers to get the product. For example, with 4 5 {\displaystyle 4^{5}} 4^{5}, you'd start with 4 ∗ 4 ∗ 4 ∗ 4 ∗ 4 {\displaystyle 4*4*4*4*4} 4*4*4*4*4 This looks daunting, but just take it one step at a time. Start by multiplying the first two fours. Then replace the two fours with the answer as shown here: 4 5 = 4 ∗ 4 ∗ 4 ∗ 4 ∗ 4 {\displaystyle 4^{5}=4*4*4*4*4} 4^{5}=4*4*4*4*4 4 ∗ 4 = 16 {\displaystyle 4*4=16} 4*4=16 4 5 = 16 ∗ 4 ∗ 4 ∗ 4 {\displaystyle 4^{5}=16*4*4*4} 4^{5}=16*4*4*4

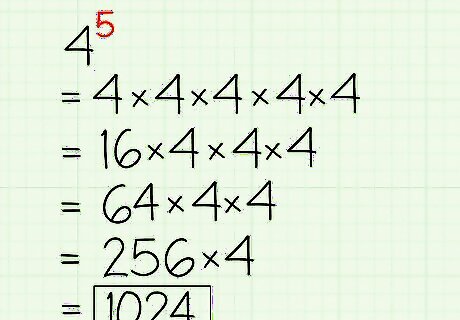
Multiply that answer to your first pair (16 here) by the next number. Keep multiplying in the numbers to "grow" your exponent. Continuing our example, you would multiple 16 by the next 4, so that: 4 5 = 16 ∗ 4 ∗ 4 ∗ 4 {\displaystyle 4^{5}=16*4*4*4} 4^{5}=16*4*4*4 16 ∗ 4 = 64 {\displaystyle 16*4=64} 16*4=64 4 5 = 64 ∗ 4 ∗ 4 {\displaystyle 4^{5}=64*4*4} 4^{5}=64*4*4 64 ∗ 4 = 256 {\displaystyle 64*4=256} 64*4=256 4 5 = 256 ∗ 4 {\displaystyle 4^{5}=256*4} 4^{5}=256*4 256 ∗ 4 = 1024 {\displaystyle 256*4=1024} 256*4=1024 As shown, you continue multiplying the base by your product of each first pair of numbers until you get your final answer. Simply keep multiplying the first two numbers, then multiply the answer by the next number in the sequence. This works for any exponent. Once you're done with our example, you should get 4 5 = 4 ∗ 4 ∗ 4 ∗ 4 ∗ 4 = 1024 {\displaystyle 4^{5}=4*4*4*4*4=1024} 4^{5}=4*4*4*4*4=1024.

Try your hand with a few more examples, checking your answers with a calculator. 8 2 {\displaystyle 8^{2}} 8^{2} 3 4 {\displaystyle 3^{4}} 3^{4} 10 7 {\displaystyle 10^{7}} 10^{7}

Use the "exp," " x n {\displaystyle x^{n}} x^{n}" or "^" button on a calculator to do exponents. It is almost impossible to do larger exponents, like 9 15 {\displaystyle 9^{15}} 9^{{15}} by hand, but calculators can handle it with ease. The button is usually clearly labeled. The Windows Seven calculator tool can be changed to scientific calculator mode by clicking the "View" tab of the calculator and selecting "Scientific". When you want the standard calculator mode back, use "View" and select "Standard". Google the expression to check your answer. You can use the "^" button on your computer, tablet or smart phone keyboard to input an expression into Google search, which will spit out an instant answer, and suggest similar expressions to explore.

Adding, Subtracting and Multiplying Exponents

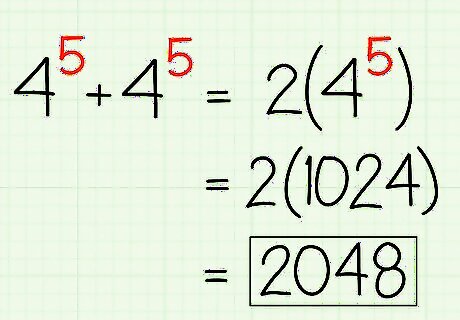
Add or subtract exponents only if they have the same base and exponent. If you have identical bases and exponents, such as 4 5 + 4 5 {\displaystyle 4^{5}+4^{5}} 4^{5}+4^{5}, you can simplify the addition of terms into simply a multiplication problem. Remember that 4 5 {\displaystyle 4^{5}} 4^{5} can be thought of as 1 ∗ 4 5 {\displaystyle 1*4^{5}} 1*4^{5} so that 4 5 + 4 5 = 1 ∗ 4 5 + 1 ∗ 4 5 = 2 ∗ 4 5 {\displaystyle 4^{5}+4^{5}=1*4^{5}+1*4^{5}=2*4^{5}} 4^{5}+4^{5}=1*4^{5}+1*4^{5}=2*4^{5} by adding, where "1 of that plus 1 of that = 2 of that", whatever "that" may be. Just add the number of similar terms (with the identical base and exponent) together and multiply the sum by that exponential expression. You can then simply solve 4 5 {\displaystyle 4^{5}} 4^{5} and multiply that answer by two. Remember, this is because multiplication is just a way to rewrite addition, since 3 + 3 = 2 ∗ 3 {\displaystyle 3+3=2*3} 3+3=2*3. Check out some examples: 3 2 + 3 2 = 2 ∗ 3 2 {\displaystyle 3^{2}+3^{2}=2*3^{2}} 3^{2}+3^{2}=2*3^{2} 4 5 + 4 5 + 4 5 = 3 ∗ 4 5 {\displaystyle 4^{5}+4^{5}+4^{5}=3*4^{5}} 4^{5}+4^{5}+4^{5}=3*4^{5} 4 5 − 4 5 + 2 = 2 {\displaystyle 4^{5}-4^{5}+2=2} 4^{5}-4^{5}+2=2 4 x 2 − 2 x 2 = 2 x 2 {\displaystyle 4x^{2}-2x^{2}=2x^{2}} 4x^{2}-2x^{2}=2x^{2}

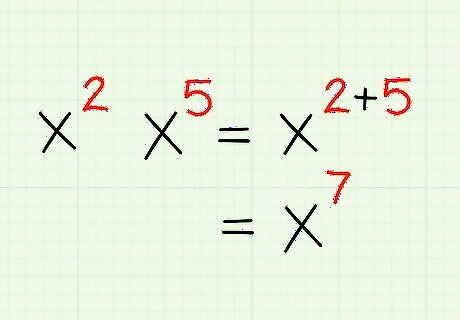
Multiply numbers with the same base by adding the exponents together. If you have two exponents with the same bass, such as x 2 ∗ x 5 {\displaystyle x^{2}*x^{5}} x^{2}*x^{5}, all you have to do is add the two exponents together with the same base. Thus, x 2 ∗ x 5 = x 7 {\displaystyle x^{2}*x^{5}=x^{7}} x^{2}*x^{5}=x^{7}. If you're confused, just break it down into all of it's parts to figure out the system: x 2 ∗ x 5 {\displaystyle x^{2}*x^{5}} x^{2}*x^{5} x 2 = x ∗ x {\displaystyle x^{2}=x*x} x^{2}=x*x x 5 = x ∗ x ∗ x ∗ x ∗ x {\displaystyle x^{5}=x*x*x*x*x} x^{5}=x*x*x*x*x x 2 ∗ x 5 = ( x ∗ x ) ∗ ( x ∗ x ∗ x ∗ x ∗ x ) {\displaystyle x^{2}*x^{5}=(x*x)*(x*x*x*x*x)} x^{2}*x^{5}=(x*x)*(x*x*x*x*x) Since everything is just the same number multiplied, we can combine them: x 2 ∗ x 5 = x ∗ x ∗ x ∗ x ∗ x ∗ x ∗ x {\displaystyle x^{2}*x^{5}=x*x*x*x*x*x*x} x^{2}*x^{5}=x*x*x*x*x*x*x x 2 ∗ x 5 = x 7 {\displaystyle x^{2}*x^{5}=x^{7}} x^{2}*x^{5}=x^{7}

Multiply an exponential number that is raised to another power, like ( x 2 ) 5 {\displaystyle (x^{2})^{5}} (x^{2})^{5}. If you have an number raised to a power, and the whole thing is then raised to a power, simply multiply the two exponents. So ( x 2 ) 5 = x 2 ∗ 5 = x 10 {\displaystyle (x^{2})^{5}=x^{2*5}=x^{10}} (x^{2})^{5}=x^{{2*5}}=x^{{10}}. Again, think of what these symbols actually mean if you get confused. ( x 2 ) 5 {\displaystyle (x^{2})^{5}} (x^{2})^{5} just means you are multiplying ( x 2 ) {\displaystyle (x^{2})} (x^{2}) by itself 5 times, so: ( x 2 ) 5 {\displaystyle (x^{2})^{5}} (x^{2})^{5} ( x 2 ) 5 = x 2 ∗ x 2 ∗ x 2 ∗ x 2 ∗ x 2 {\displaystyle (x^{2})^{5}=x^{2}*x^{2}*x^{2}*x^{2}*x^{2}} (x^{2})^{5}=x^{2}*x^{2}*x^{2}*x^{2}*x^{2} Since the base bases are the same, you can simply add them together: ( x 2 ) 5 = x 2 ∗ x 2 ∗ x 2 ∗ x 2 ∗ x 2 = x 10 {\displaystyle (x^{2})^{5}=x^{2}*x^{2}*x^{2}*x^{2}*x^{2}=x^{10}} (x^{2})^{5}=x^{2}*x^{2}*x^{2}*x^{2}*x^{2}=x^{{10}}

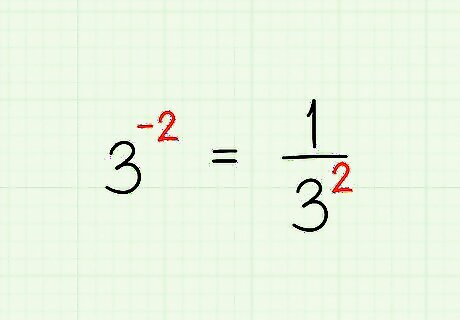
Treat negative exponents like fractions, or the number's reciprocal. If you don't know what reciprocals are, it is okay. If you have a negative exponent, like 3 − 2 {\displaystyle 3^{-2}} 3^{{-2}}, simply make the exponent positive and put it under one, ending up with 1 3 2 {\displaystyle {\frac {1}{3^{2}}}} {\frac {1}{3^{2}}}. Check out a few more examples: 5 − 10 1 5 10 {\displaystyle 5^{-10}{\frac {1}{5^{10}}}} 5^{{-10}}{\frac {1}{5^{{10}}}} 3 x − 4 = 3 x 4 {\displaystyle 3x^{-}4={\frac {3}{x^{4}}}} 3x^{-}4={\frac {3}{x^{4}}}

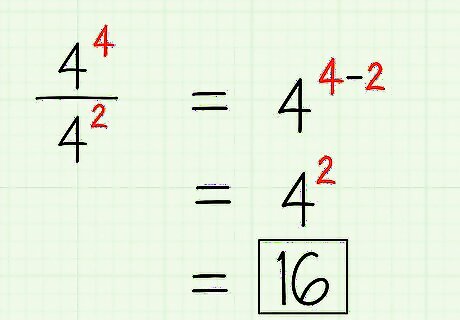
Divide two numbers with the same base by subtracting the exponents. Division is the opposite of multiplication, and while they aren't always solved exactly opposite, they are here. If you have the equation 4 4 4 2 {\displaystyle {\frac {4^{4}}{4^{2}}}} {\frac {4^{4}}{4^{2}}}, simply subtract the top exponent by the bottom and leave the base the same. Thus, 4 4 4 2 = 4 4 − 2 = 4 2 {\displaystyle {\frac {4^{4}}{4^{2}}}=4^{4-2}=4^{2}} {\frac {4^{4}}{4^{2}}}=4^{{4-2}}=4^{2}, or 16. As you'll soon see, any number that is part of a fraction, like 1 4 2 {\displaystyle {\frac {1}{4^{2}}}} {\frac {1}{4^{2}}}, can actually be rewritten as 4 − 2 {\displaystyle 4^{-2}} 4^{{-2}}. Negative exponents create fractions.

Try out some practice problems to get use to manipulating exponential numbers. The following problems cover everything currently shown. To see the answer, simply highlight the entire line the problem is on. 5 3 {\displaystyle 5^{3}} 5^{3} = 125 2 2 + 2 2 + 2 2 {\displaystyle 2^{2}+2^{2}+2^{2}} 2^{2}+2^{2}+2^{2} = 12 x 1 2 − 2 x 1 2 {\displaystyle x^{1}2-2x^{1}2} x^{1}2-2x^{1}2 = -x^12 y 3 ∗ y {\displaystyle y^{3}*y} y^{3}*y = y 4 {\displaystyle y^{4}} y^{4} Remember, a number without a power has an exponent of 1 ( Q 3 ) 5 {\displaystyle (Q^{3})^{5}} (Q^{3})^{5} = Q 1 5 {\displaystyle Q^{1}5} Q^{1}5 r 5 r 2 {\displaystyle {\frac {r^{5}}{r^{2}}}} {\frac {r^{5}}{r^{2}}} = r 3 {\displaystyle r^{3}} r^{3}

Solving Fractional Exponents

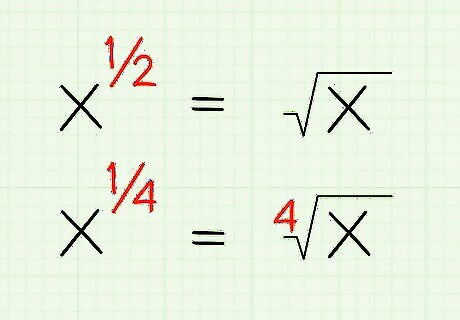
Treat fractional exponents, like x 1 2 {\displaystyle x^{\frac {1}{2}}} x^{{{\frac {1}{2}}}} like a square root problem. x 1 2 {\displaystyle x^{\frac {1}{2}}} x^{{{\frac {1}{2}}}} is actually the exact same thing as x {\displaystyle {\sqrt {x}}} {\sqrt {x}}. This is done similarly no matter what the bottom of the fraction is, so x 1 4 {\displaystyle x^{\frac {1}{4}}} x^{{{\frac {1}{4}}}} would be the 4th root of x, also written as x 4 {\displaystyle {\sqrt[{4}]{x}}} {\sqrt[ {4}]{x}}. Roots are the inverse of exponents. For example, if you took the answer to x 4 {\displaystyle {\sqrt[{4}]{x}}} {\sqrt[ {4}]{x}} raised it to the fourth power, you would be back at x {\displaystyle x} x, such as 16 4 = 2 {\displaystyle {\sqrt[{4}]{16}}=2} {\sqrt[ {4}]{16}}=2 can be checked as 2 4 = 16 {\displaystyle 2^{4}=16} 2^{4}=16. Also for example, if x 4 = 2 {\displaystyle {\sqrt[{4}]{x}}=2} {\sqrt[ {4}]{x}}=2 then 2 4 = x {\displaystyle 2^{4}=x} 2^{4}=x therefore x = 2 {\displaystyle x=2} x=2 .

Turn the top number into a normal exponent for mixed fractions. x 5 3 {\displaystyle x^{\frac {5}{3}}} x^{{{\frac {5}{3}}}} might look impossible, but it is easy if you remember how exponents are multiplied. Simply turn the base into a root, like a normal fraction, then raise the whole thing to the power on the top of the fraction. If you're struggling to remember this, think through the theory. For example: x 5 3 {\displaystyle x^{\frac {5}{3}}} x^{{{\frac {5}{3}}}} x 5 3 = ( x 5 ) 1 3 {\displaystyle x^{\frac {5}{3}}=(x^{5})^{\frac {1}{3}}} {\displaystyle x^{\frac {5}{3}}=(x^{5})^{\frac {1}{3}}} or x 5 3 = ( x 1 3 ) 5 {\displaystyle x^{\frac {5}{3}}=(x^{\frac {1}{3}})^{5}} {\displaystyle x^{\frac {5}{3}}=(x^{\frac {1}{3}})^{5}} x 1 3 = x 3 {\displaystyle x^{\frac {1}{3}}={\sqrt[{3}]{x}}} x^{{{\frac {1}{3}}}}={\sqrt[ {3}]{x}} x 5 3 {\displaystyle x^{\frac {5}{3}}} x^{{{\frac {5}{3}}}} = ( x 3 ) 5 {\displaystyle ({\sqrt[{3}]{x}})^{5}} ({\sqrt[ {3}]{x}})^{5}

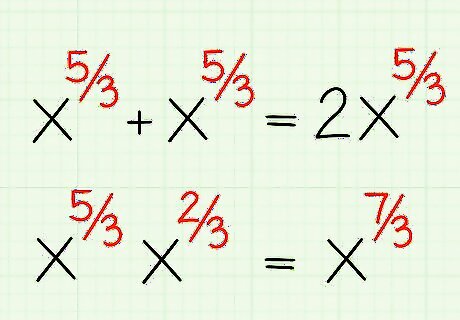
Add, subtract, and multiply fractional exponents just like normal. It is much easier to try and add and subtract your exponents before solving them or turning them into roots. If the base is the same and the exponent identical, you can add and subtract like normal. If the base is the same, you can multiply and divide the exponents like normal as well, as long as your remember how to add and subtract fractions. For example: x 5 3 + x 5 3 = 2 ( x 5 3 ) {\displaystyle x^{\frac {5}{3}}+x^{\frac {5}{3}}=2(x^{\frac {5}{3}})} x^{{{\frac {5}{3}}}}+x^{{{\frac {5}{3}}}}=2(x^{{{\frac {5}{3}}}}) x 5 3 ∗ x 2 3 = x 7 3 {\displaystyle x^{\frac {5}{3}}*x^{\frac {2}{3}}=x^{\frac {7}{3}}} x^{{{\frac {5}{3}}}}*x^{{{\frac {2}{3}}}}=x^{{{\frac {7}{3}}}}