
views

Partition your number. Separate the number you want to find the nth root of into n-digit intervals before and after the decimal. If there are fewer than n digits before the decimal, then that is the first interval. And if there are no digits or fewer than n digits after the decimal, fill in the spaces with zeroes.
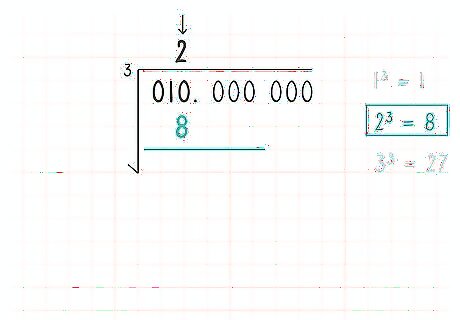
Find an initial estimate. Find a number (a) raised to the nth power closest to the first n digits (or the fewer than n digits before the decimal) as a base-ten number without going over. This is the first and only digit of your estimate so far.
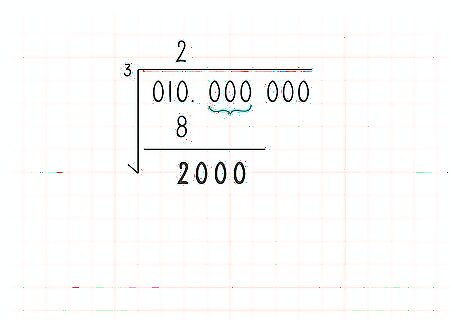
Modify the difference. Subtract your estimate to the nth power (a) from those first n digits and bring down the next n digits next to that difference to form a new number, a modified difference. (Or multiply the difference by 10 and add the next n digits as a base-ten number.)
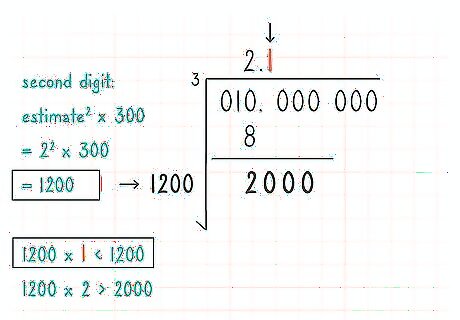
Find the second digit of your estimate. Find a number b such that (nC1 a (10) + nC2 a b (10) ) + . . . + nCn - 1 a b (10 ) + nCn b (10 ) )b is less than or equal to the modified difference above (10 (d ) + d1d2. . . dn). This becomes the second digit of your estimate so far. The combinations notation nCr represents n! divided by the product of (n - r)! and r!, where n! = n(n - 1)(n - 2)(n - 3) . . . (3)(2)(1). The notation nCr is sometimes expressed as n over r within tall parentheses without a division bar, and it can be calculated simply as the first r factors of n! divided by r!, which is often written as nPr divided by r!

Find your new modified difference. Subtract the two quantities in the last step above (10 (d ) + d1d2. . . dn minus nC1 a (10) + nC2 a b (10) ) + . . . + nCn - 1 a b (10 ) + nCn b (10 ) )b) to form your new modified difference by bringing down the next set of n digits next to that result. (Or multiply the difference by 10 and add the next n digits as a base-ten number.)
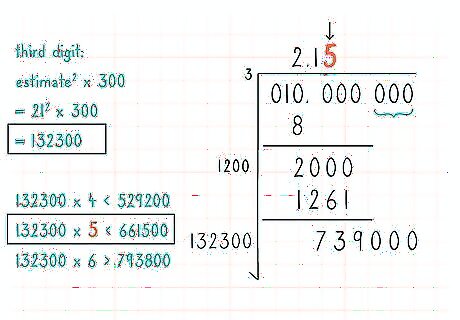
Find the third digit of your estimate. Find a new number c and use your estimate so far, a (which is now 2 digits), such that (nC1 a (10) + nC2 a c (10 ) + . . . + nCn - 1 a c (10 ) + nCn c (10 ) ) c is less than or equal to the new modified difference in above (10 (d ) + d1d2. . . dn). This becomes the third digit of your estimate so far.

Repeat. Keep repeating the last two steps above to find more digits of your estimate. This is basically a rolling binomial expansion minus the lead term, where the two terms involved are the prior estimate multiplied by 10 and the next digit to improve the estimate.

















Comments
0 comment