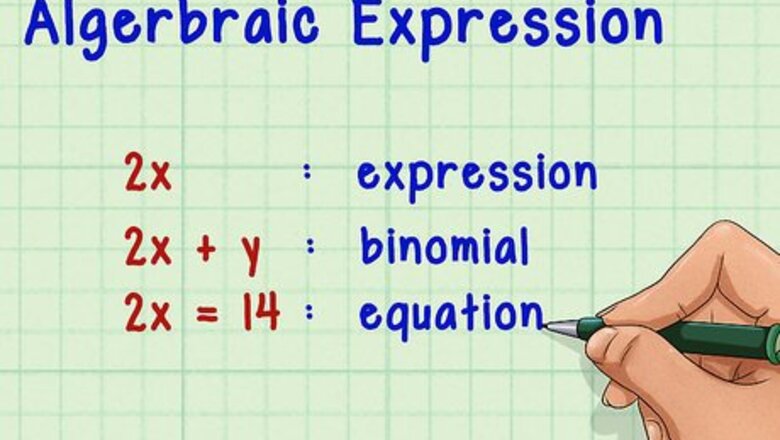
views
Understanding an Expression

Identify the parts of an algebraic expression. An algebraic expression is a set of numbers and letters combined by mathematical operations, such as addition, subtraction, division, and multiplication. The numbers in the expression are called constants or coefficients, depending on their function. The letters are called variables. 2 x {\displaystyle 2x} 2x is an expression. In this expression, you are multiplying the coefficient 2 {\displaystyle 2} 2 by the variable x {\displaystyle x} x. 2 x + 3 y {\displaystyle 2x+3y} 2x+3y is an expression called a binomial. In this expression, you add the product of 3 y {\displaystyle 3y} 3y to the product of 2 x {\displaystyle 2x} 2x. In this expression, 2 {\displaystyle 2} 2 and 3 {\displaystyle 3} 3 are coefficients, and x {\displaystyle x} x and y {\displaystyle y} y are variables. Once you add an equal sign to an expression, it becomes an equation. For example, 2 x = 14 {\displaystyle 2x=14} 2x=14 is an equation.
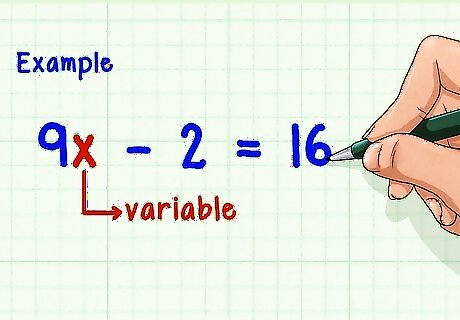
Understand what a variable is. A variable is a letter that represents any number. Therefore, variables are often used to represent unknown numbers. In algebra, you are usually trying to find the value of the variable. In order to evaluate an algebraic expression, however, you need to be given the variable’s value.
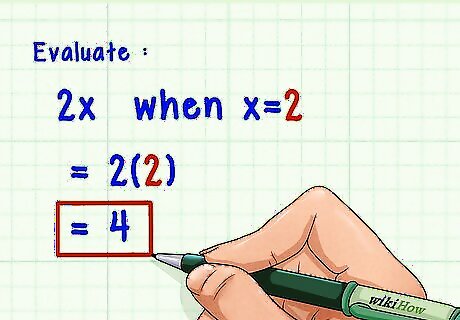
Determine how to evaluate the expression. Evaluate means to simplify an expression. When you are asked to evaluate an algebraic expression, you need to plug a given value for the variable into the expression and solve. For example, you might be asked to evaluate 2 x {\displaystyle 2x} 2x when x = 2 {\displaystyle x=2} x=2.
Evaluating an Expression with One or Two Variables
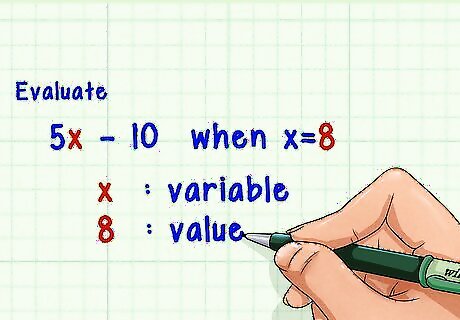
Identify the variable and its value. This information should be given to you. Usually you will be told to evaluate the expression “when” or “where” the variable is equal to a certain value. If you are not given the variable’s value, you cannot evaluate the expression. For example, you might be asked to evaluate the expression 5 x − 10 {\displaystyle 5x-10} 5x-10 when x = 8 {\displaystyle x=8} x=8.
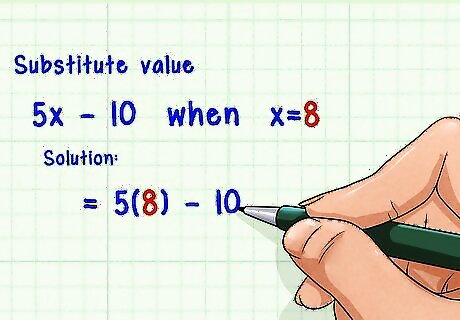
Substitute the given value for the variable. To do this, plug the given value into the expression wherever you see the variable. If the variable has a coefficient (a number you need to multiply its value by), make sure to put the value in parentheses. For example, to evaluate 5 x − 10 {\displaystyle 5x-10} 5x-10 when x = 8 {\displaystyle x=8} x=8, replace the x {\displaystyle x} x in the equation with 8 {\displaystyle 8} 8: 5 ( 8 ) − 10 {\displaystyle 5(8)-10} 5(8)-10.

Complete the necessary calculations. Remember to follow the order of operations when solving an expression. When you complete your calculations rewrite the expression as an equation. For example: 5 ( 8 ) − 10 {\displaystyle 5(8)-10} 5(8)-10 = 40 − 10 {\displaystyle =40-10} =40-10 = 30 {\displaystyle =30} =30So, 5 ( 8 ) − 10 = 30 {\displaystyle 5(8)-10=30} 5(8)-10=30.
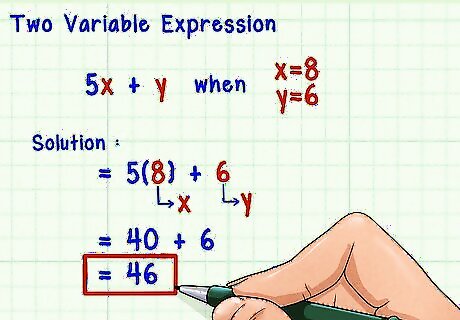
Evaluate an expression with Two Variables. To do this, follow the same steps as you do for evaluating an expression with one variable, except plug in the values for both variables into the equation. These values should be given. Make sure you do not switch the values. The x {\displaystyle x} x value cannot be substituted for the y {\displaystyle y} y variable and vice versa. Doing so will give you an incorrect solution.
Completing Sample Problems
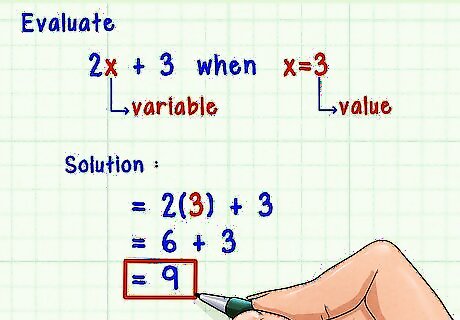
Evaluate the following expression when x = 3 {\displaystyle x=3} x=3: 2 x + 3 {\displaystyle 2x+3} 2x+3. Identify the variable and its value. The variable is x {\displaystyle x} x, and you are evaluating the expression for x = 3 {\displaystyle x=3} x=3. Substitute the given value for the variable: 2 ( 3 ) + 3 {\displaystyle 2(3)+3} 2(3)+3. Make the necessary calculations: 2 ( 3 ) + 3 = 6 + 3 = 9 {\displaystyle 2(3)+3=6+3=9} 2(3)+3=6+3=9. Write the equation: 2 ( 3 ) + 3 = 9 {\displaystyle 2(3)+3=9} 2(3)+3=9
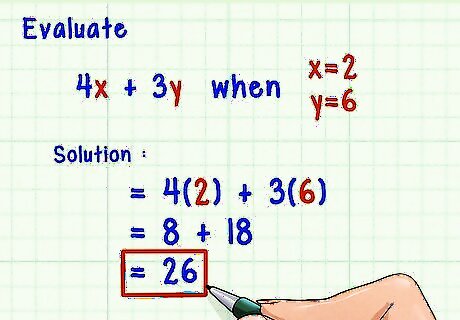
Evaluate the following expression with two variables when x = 2 {\displaystyle x=2} x=2 and y = 6 {\displaystyle y=6} y=6: 4 x + 3 y {\displaystyle 4x+3y} 4x+3y. Identify both variables and their values. The variables are x {\displaystyle x} x and y {\displaystyle y} y, and you are evaluating the expression for x = 2 {\displaystyle x=2} x=2 and y = 6 {\displaystyle y=6} y=6. Substitute both given values for the variables: 4 ( 2 ) + 3 ( 6 ) {\displaystyle 4(2)+3(6)} 4(2)+3(6). Make the necessary calculations: 4 ( 2 ) + 3 ( 6 ) = 8 + 18 = 26 {\displaystyle 4(2)+3(6)=8+18=26} 4(2)+3(6)=8+18=26. Write the equation: 4 ( 2 ) + 3 ( 6 ) = 26 {\displaystyle 4(2)+3(6)=26} 4(2)+3(6)=26.

Evaluate the following polynomial when x = 4 {\displaystyle x=4} x=4: 7 x 2 − 12 x + 13 {\displaystyle 7x^{2}-12x+13} 7x^{{2}}-12x+13. Identify the variable and its value. The variable is x {\displaystyle x} x, and you are evaluating the expression for x = 4 {\displaystyle x=4} x=4. Substitute the given value for the variable: 7 ( 4 ) 2 − 12 ( 4 ) + 13 {\displaystyle 7(4)^{2}-12(4)+13} 7(4)^{{2}}-12(4)+13. Make the necessary calculations. Remember when working with exponents that you should calculate the exponent before multiplying by a coefficient: 7 ( 4 ) 2 − 12 ( 4 ) + 13 {\displaystyle 7(4)^{2}-12(4)+13} 7(4)^{{2}}-12(4)+13 = 7 ( 16 ) − 12 ( 4 ) + 13 {\displaystyle =7(16)-12(4)+13} =7(16)-12(4)+13 = 112 − 48 + 13 {\displaystyle =112-48+13} =112-48+13 = 64 + 13 {\displaystyle =64+13} =64+13 = 77 {\displaystyle =77} =77 Write the equation: 7 ( 16 ) − 12 ( 4 ) + 13 = 77 {\displaystyle 7(16)-12(4)+13=77} 7(16)-12(4)+13=77
















Comments
0 comment