How to Convert Radians to Degrees

Tech16

Editor

posted on 12 years ago — updated on 1 second ago

29
views

Radians and degrees are both units used for measuring angles. As you may know, a circle is comprised of 2π radians, which is the equivalent of 360°; both of these values represent going "once around" a circle. Therefore, 1π radian represents going 180° around a circle, which makes 180/π the perfect conversion tool for moving from radians to degrees. To convert from radians to degrees, you simply have to multiply the radian value by 180/π. If you want to know how to do this, and to understand the concept in the process, read this article.

Steps

Know that π radians is equal to 180 degrees. Before you begin the conversion process, you have to know that π radians = 180°, which is equivalent to going halfway around a circle. This is important because you'll be using 180/π as a conversion metric. This is because 1 radians is equal to 180/π degrees.

Multiply the radians by 180/π to convert to degrees. It's that simple. Let's say you're working with π/12 radians. Then, you've got to multiply it by 180/π and simplify when necessary. Here's how you do it: π/12 x 180/π = 180π/12π ÷ 12π/12π = 15° π/12 radians = 15°

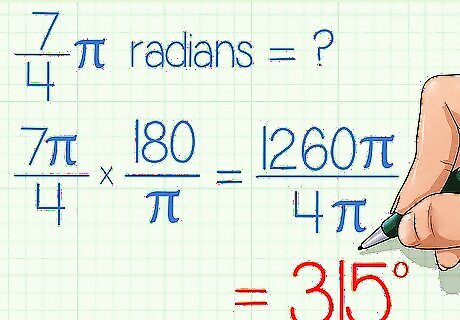
Practice with a few examples. If you really want to get the hang of it, then try converting from radians to degrees with a few more examples. Here are some other problems you can do: Example 1: 1/3π radians = π/3 x 180/π = 180π/3π ÷ 3π/3π = 60° Example 2: 7/4π radians = 7π/4 x 180/π = 1260π/4π ÷ 4π/4π = 315° Example 3: 1/2π radians = π /2 x 180/π = 180π /2π ÷ 2π/2π = 90°

Remember that there's a difference between "radians" and "π radians." If you say 2π radians or 2 radians, you are not using the same terms. As you know, 2π radians is equal to 360 degrees, but if you're working with 2 radians, then if you want to convert it to degrees, you will have to calculate 2 x 180/π. You will get 360/π, or 114.5°. This is a different answer because, if you're not working with π radians, the π does not cancel out in the equation and results in a different value.