How to Calculate Variance

Calculating Sample Variance

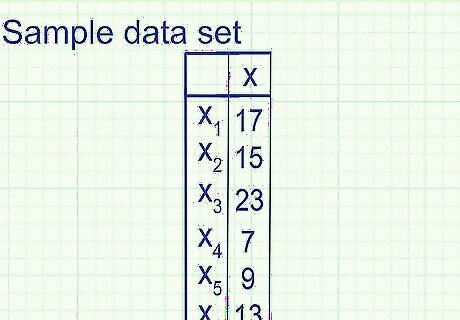
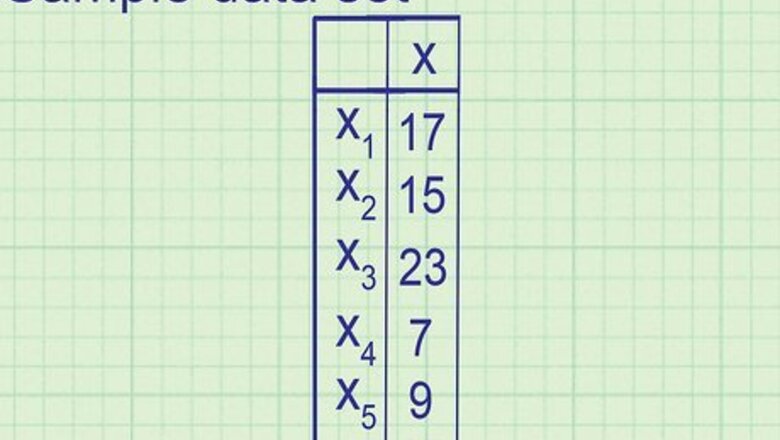
Use the sample variance formula if you're working with a partial data set. In most cases, statisticians only have access to a sample, or a subset of the population they're studying. For example, instead of analyzing the population "cost of every car in Germany," a statistician could find the cost of a random sample of a few thousand cars. He can use this sample to get a good estimate of German car costs, but it will likely not match the actual numbers exactly. Example: Analyzing the number of muffins sold each day at a cafeteria, you sample six days at random and get these results: 38, 37, 36, 28, 18, 14, 12, 11, 10.7, 9.9. This is a sample, not a population, since you don't have data on every single day the cafeteria was open. If you have every data point in a population, skip down to the method below instead.

Write down the sample variance formula. The variance of a data set tells you how spread out the data points are. The closer the variance is to zero, the more closely the data points are clustered together. When working with sample data sets, use the following formula to calculate variance: s 2 {\displaystyle s^{2}} s^{2} = /(n - 1) s 2 {\displaystyle s^{2}} s^{2} is the variance. Variance is always measured in squared units. x i {\displaystyle x_{i}} x_{i} represents a term in your data set. ∑, meaning "sum," tells you to calculate the following terms for each value of x i {\displaystyle x_{i}} x_{i}, then add them together. x̅ is the mean of the sample. n is the number of data points.

Calculate the mean of the sample. The symbol x̅ or "x-bar" refers to the mean of a sample. Calculate this as you would any mean: add all the data points together, then divide by the number of data points. Example: First, add your data points together: 17 + 15 + 23 + 7 + 9 + 13 = 84Next, divide your answer by the number of data points, in this case six: 84 ÷ 6 = 14.Sample mean = x̅ = 14. You can think of the mean as the "center-point" of the data. If the data clusters around the mean, variance is low. If it is spread out far from the mean, variance is high.

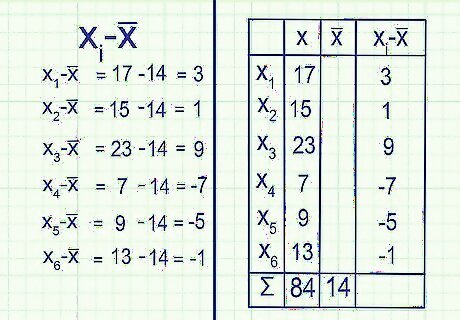
Subtract the mean from each data point. Now it's time to calculate x i {\displaystyle x_{i}} x_{i} - x̅, where x i {\displaystyle x_{i}} x_{i} is each number in your data set. Each answer tells you that number's deviation from the mean, or in plain language, how far away it is from the mean. Example: x 1 {\displaystyle x_{1}} x_{1} - x̅ = 17 - 14 = 3 x 2 {\displaystyle x_{2}} x_{2} - x̅ = 15 - 14 = 1 x 3 {\displaystyle x_{3}} x_{3} - x̅ = 23 - 14 = 9 x 4 {\displaystyle x_{4}} x_{4} - x̅ = 7 - 14 = -7 x 5 {\displaystyle x_{5}} x_{5} - x̅ = 9 - 14 = -5 x 6 {\displaystyle x_{6}} x_{6} - x̅ = 13 - 14 = -1 It's easy to check your work, as your answers should add up to zero. This is due to the definition of mean, since the negative answers (distance from mean to smaller numbers) exactly cancel out the positive answers (distance from mean to larger numbers).

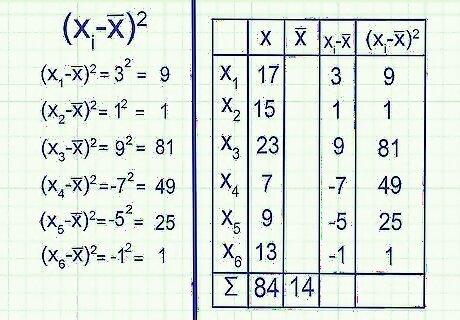
Square each result. As noted above, your current list of deviations ( x i {\displaystyle x_{i}} x_{i} - x̅) sum up to zero. This means the "average deviation" will always be zero as well, so that doesn't tell use anything about how spread out the data is. To solve this problem, find the square of each deviation. This will make them all positive numbers, so the negative and positive values no longer cancel out to zero. Example:( x 1 {\displaystyle x_{1}} x_{1} - x̅) 2 = 3 2 = 9 {\displaystyle ^{2}=3^{2}=9} ^{2}=3^{2}=9 ( x 2 {\displaystyle (x_{2}} (x_{2} - x̅) 2 = 1 2 = 1 {\displaystyle ^{2}=1^{2}=1} ^{2}=1^{2}=19 = 81(-7) = 49(-5) = 25(-1) = 1 You now have the value ( x i {\displaystyle x_{i}} x_{i} - x̅) 2 {\displaystyle ^{2}} ^{2} for each data point in your sample.

Find the sum of the squared values. Now it's time to calculate the entire numerator of the formula: ∑[( x i {\displaystyle x_{i}} x_{i} - x̅) 2 {\displaystyle ^{2}} ^{2}]. The upper-case sigma, ∑, tells you to sum the value of the following term for each value of x i {\displaystyle x_{i}} x_{i}. You've already calculated ( x i {\displaystyle x_{i}} x_{i} - x̅) 2 {\displaystyle ^{2}} ^{2} for each value of x i {\displaystyle x_{i}} x_{i} in your sample, so all you need to do is add the results of all of the squared deviations together. Example: 9 + 1 + 81 + 49 + 25 + 1 = 166.

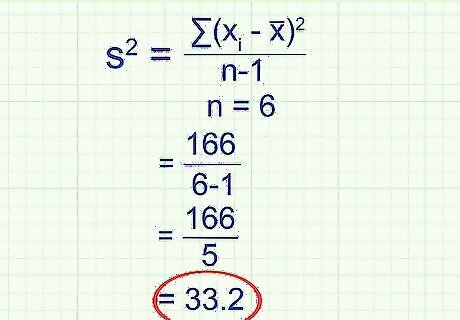
Divide by n - 1, where n is the number of data points. A long time ago, statisticians just divided by n when calculating the variance of the sample. This gives you the average value of the squared deviation, which is a perfect match for the variance of that sample. But remember, a sample is just an estimate of a larger population. If you took another random sample and made the same calculation, you would get a different result. As it turns out, dividing by n - 1 instead of n gives you a better estimate of variance of the larger population, which is what you're really interested in. This correction is so common that it is now the accepted definition of a sample's variance. Example: There are six data points in the sample, so n = 6.Variance of the sample = s 2 = 166 6 − 1 = {\displaystyle s^{2}={\frac {166}{6-1}}=} s^{2}={\frac {166}{6-1}}= 33.2

Understand variance and standard deviation. Note that, since there was an exponent in the formula, variance is measured in the squared unit of the original data. This can make it difficult to understand intuitively. Instead, it's often useful to use the standard deviation. You didn't waste your effort, though, as the standard deviation is defined as the square root of the variance. This is why the variance of a sample is written s 2 {\displaystyle s^{2}} s^{2}, and the standard deviation of a sample is s {\displaystyle s} s. For example, the standard deviation of the sample above = s = √33.2 = 5.76.

Calculating Population Variance

Use the population variance formula if you've collected data from every point in the population. The term "population" refers to the total set of relevant observations. For example, if you're studying the age of Texas residents, your population would include the age of every single Texas resident. You would normally create a spreadsheet for a large data set like that, but here's a smaller example data set: Example: There are exactly six fish tanks in a room of the aquarium. The six tanks contain the following numbers of fish: x 1 = 5 {\displaystyle x_{1}=5} x_{1}=5 x 2 = 5 {\displaystyle x_{2}=5} x_{2}=5 x 3 = 8 {\displaystyle x_{3}=8} x_{3}=8 x 4 = 12 {\displaystyle x_{4}=12} x_{4}=12 x 5 = 15 {\displaystyle x_{5}=15} x_{5}=15 x 6 = 18 {\displaystyle x_{6}=18} x_{6}=18

Write down the population variance formula. Since a population contains all the data you need, this formula gives you the exact variance of the population. In order to distinguish it from sample variance (which is only an estimate), statisticians use different variables: σ 2 {\displaystyle ^{2}} ^{2} = /n σ 2 {\displaystyle ^{2}} ^{2} = population variance. This is a lower-case sigma, squared. Variance is measured in squared units. x i {\displaystyle x_{i}} x_{i} represents a term in your data set. The terms inside ∑ will be calculated for each value of x i {\displaystyle x_{i}} x_{i}, then summed. μ is the population mean n is the number of data points in the population

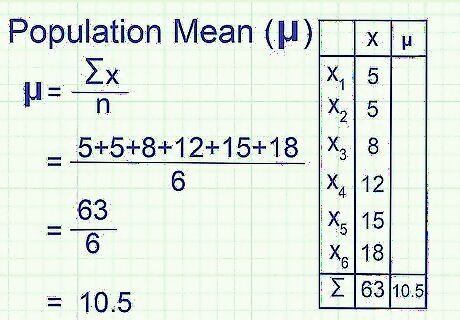
Find the mean of the population. When analyzing a population, the symbol μ ("mu") represents the arithmetic mean. To find the mean, add all the data points together, then divide by the number of data points. You can think of the mean as the "average," but be careful, as that word has multiple definitions in mathematics. Example: mean = μ = 5 + 5 + 8 + 12 + 15 + 18 6 {\displaystyle {\frac {5+5+8+12+15+18}{6}}} {\frac {5+5+8+12+15+18}{6}} = 10.5

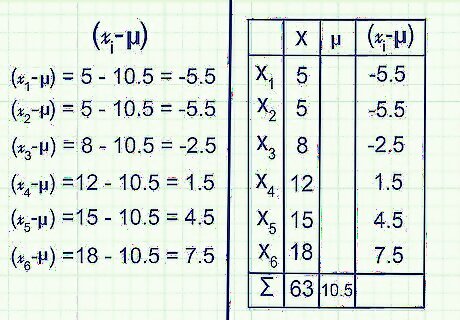
Subtract the mean from each data point. Data points close to the mean will result in a difference closer to zero. Repeat the subtraction problem for each data point, and you might start to get a sense of how spread out the data is. Example: x 1 {\displaystyle x_{1}} x_{1} - μ = 5 - 10.5 = -5.5 x 2 {\displaystyle x_{2}} x_{2} - μ = 5 - 10.5 = -5.5 x 3 {\displaystyle x_{3}} x_{3} - μ = 8 - 10.5 = -2.5 x 4 {\displaystyle x_{4}} x_{4} - μ = 12 - 10.5 = 1.5 x 5 {\displaystyle x_{5}} x_{5} - μ = 15 - 10.5 = 4.5 x 6 {\displaystyle x_{6}} x_{6} - μ = 18 - 10.5 = 7.5

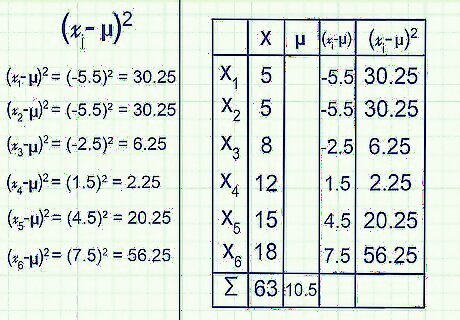
Square each answer. Right now, some of your numbers from the last step will be negative, and some will be positive. If you picture your data on a number line, these two categories represent numbers to the left of the mean, and numbers to the right of the mean. This is no good for calculating variance, since these two groups will cancel each other out. Square each number so they are all positive instead. Example:( x i {\displaystyle x_{i}} x_{i} - μ) 2 {\displaystyle ^{2}} ^{2} for each value of i from 1 to 6:(-5.5) 2 {\displaystyle ^{2}} ^{2} = 30.25(-5.5) 2 {\displaystyle ^{2}} ^{2} = 30.25(-2.5) 2 {\displaystyle ^{2}} ^{2} = 6.25(1.5) 2 {\displaystyle ^{2}} ^{2} = 2.25(4.5) 2 {\displaystyle ^{2}} ^{2} = 20.25(7.5) 2 {\displaystyle ^{2}} ^{2} = 56.25

Find the mean of your results. Now you have a value for each data point, related (indirectly) to how far that data point is from the mean. Take the mean of these values by adding them all together, then dividing by the number of values. Example:Variance of the population = 30.25 + 30.25 + 6.25 + 2.25 + 20.25 + 56.25 6 = 145.5 6 = {\displaystyle {\frac {30.25+30.25+6.25+2.25+20.25+56.25}{6}}={\frac {145.5}{6}}=} {\frac {30.25+30.25+6.25+2.25+20.25+56.25}{6}}={\frac {145.5}{6}}= 24.25

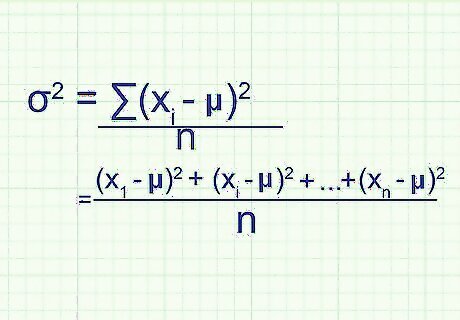
Relate this back to the formula. If you're not sure how this matches the formula at the beginning of this method, try writing out the whole problem in longhand: After finding the difference from the mean and squaring, you have the value ( x 1 {\displaystyle x_{1}} x_{1} - μ) 2 {\displaystyle ^{2}} ^{2}, ( x 2 {\displaystyle x_{2}} x_{2} - μ) 2 {\displaystyle ^{2}} ^{2}, and so on up to ( x n {\displaystyle x_{n}} x_{n} - μ) 2 {\displaystyle ^{2}} ^{2}, where x n {\displaystyle x_{n}} x_{n} is the last data point in the set. To find the mean of these values, you sum them up and divide by n: ( ( x 1 {\displaystyle x_{1}} x_{1} - μ) 2 {\displaystyle ^{2}} ^{2} + ( x 2 {\displaystyle x_{2}} x_{2} - μ) 2 {\displaystyle ^{2}} ^{2} + ... + ( x n {\displaystyle x_{n}} x_{n} - μ) 2 {\displaystyle ^{2}} ^{2} ) / n After rewriting the numerator in sigma notation, you have /n, the formula for variance.