How to Calculate Multiple Dice Probabilities

Enumeration

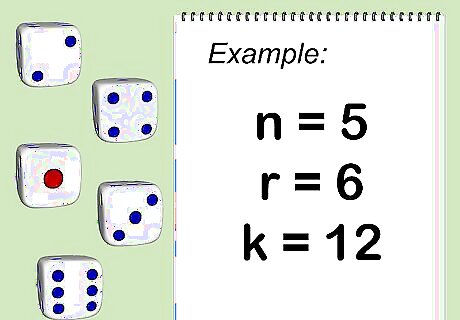
Note the number of dice, their sides, and the desired sum.

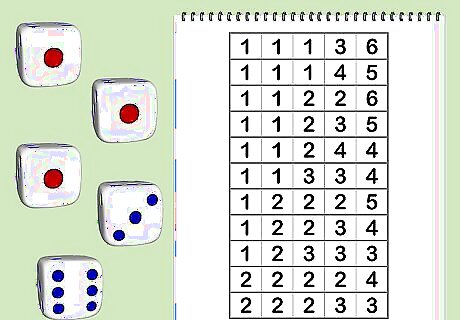
Enumerate all the ways that sum can be reached. This can be tedious for large numbers of dice, but is fairly straightforward. This is equivalent to the finding all partitions of k into exactly n parts with no part larger than r. An example for n=5, r=6, and k=12 is shown as an example. In order to ensure that the count is both exhaustive and that no partition is counted twice, the partitions are presented in lexicographic order and the dice in each partition in non-decreasing order.

Not all partitions listed in the previous step are equally likely. This is why they must be listed, not simply counted. In a smaller 3 die example, the partition 123 covers 6 possibilities (123, 132, 213, 231, 312, 321) while the partition 114 covers only 3 (114, 141, 411) and 222 only includes itself. Use the multinomial formula to compute the number of ways to permute the digits in each partition. This information has been added to the table from the previous section.

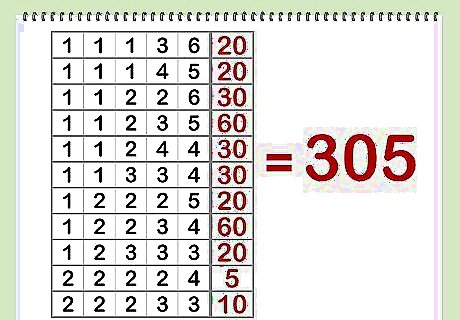
Add the total number of ways to get the desired sum.

Divide by the total number of outcomes. Since each die has r equally probable faces, this is simply r.

Recursion

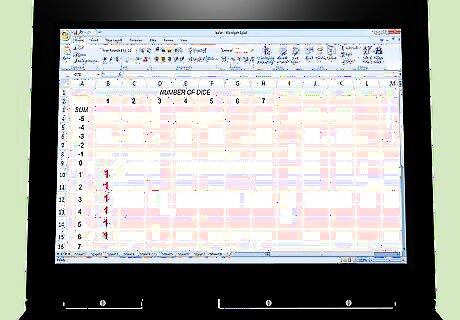
Note the probabilities of the outcomes of a single die. Record them in a spreadsheet. The example shown uses 6-sided dice. The blank rows for negative sums are treated as zeros and allow the same formula to be used in all rows.

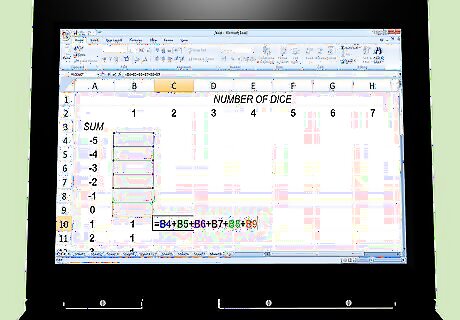
In the column for 2 dice, use the formula shown. That is, the probability of 2 dice showing any sum k equals the sum of the following events. For very high or low values of k, some or all or these terms might be zero, but the formula is valid for all k. First die shows k-1 and the second shows 1. First die shows k-2 and the second shows 2. First die shows k-3 and the second shows 3. First die shows k-4 and the second shows 4. First die shows k-5 and the second shows 5. First die shows k-6 and the second shows 6.

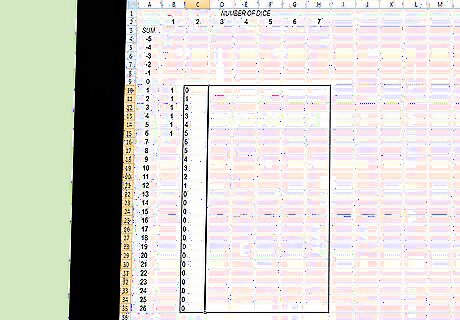
Likewise, for three or more dice, the same formula still applies, using the now known probabilities for each given sum on one die fewer. Thus, the formula entered in step two can be filled both down and across until the table includes as much data as required.

The spreadsheet shown computed "number of ways" not "probability", but converting between them is easy: probability = number of ways / r^n where r is number of sides on each die and n is the number of dice. Alternatively, the spreadsheet can be modified to compute probability directly.

Generating Functions

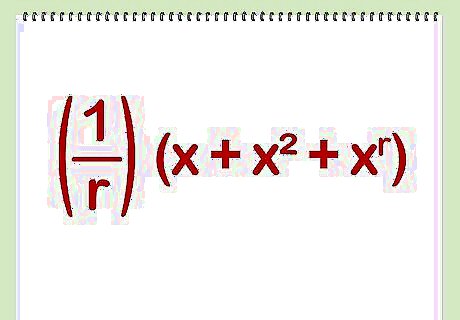
Write the polynomial, (1/r)(x + x + ... + x). This is the generating function for a single die. The coefficient of the x term is the probability that the die shows k.

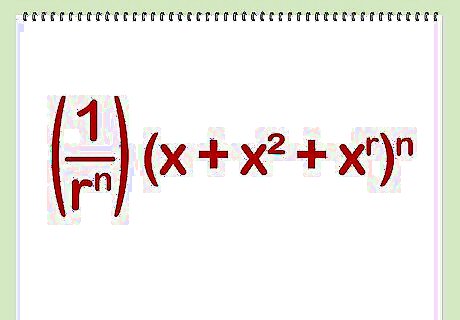
Raise this polynomial to the n power to get the corresponding generating function for the sum shown on n dice. That is compute (1/r)(x + x + ... + x). If n is larger than about 2, you'll probably want to do this on a computer.

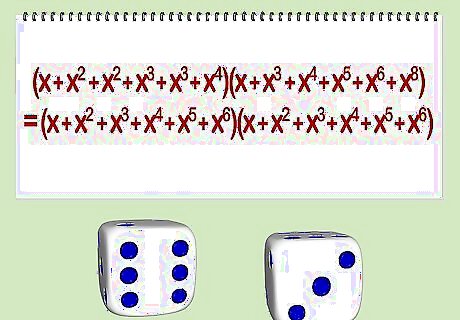
Computationally, this is equivalent to the previous method, but sometimes theoretical results are easier to derive with a generating function. For example throwing two regular 6-sided dice has exactly the same distribution of sums as a die labeled (1, 2, 2, 3, 3, 4) and another labeled (1, 3, 4, 5, 6, 8). This is because (x+x +x+x+x+x)(x+x +x+x+x+x) = (x+x +x+x+x+x)(x+x +x+x+x+x).

Continuous Approximation

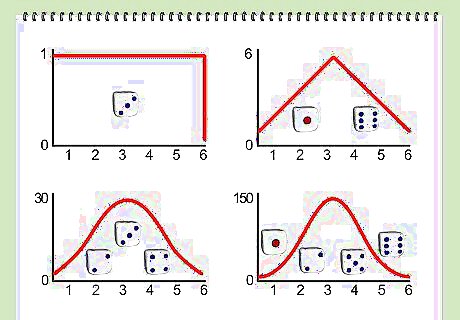
For a large number of dice, exact computation by the above methods may be difficult. The central limit theorem states that the sum of a number of identical dice approaches a normal distribution as the number of dice increases.

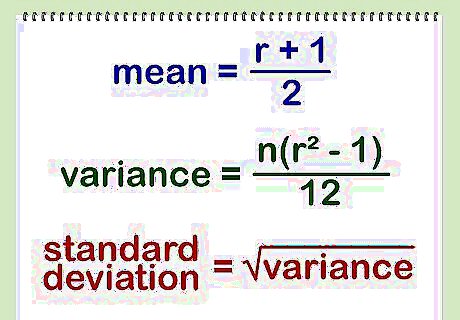
Compute the mean and standard variation based on the number and type of dice. Assuming n dice numbered 1 to r, the formulas below apply. The mean is (r+1)/2. The variance is n(r^2-1)/12. The standard deviation is the square root of the variance.

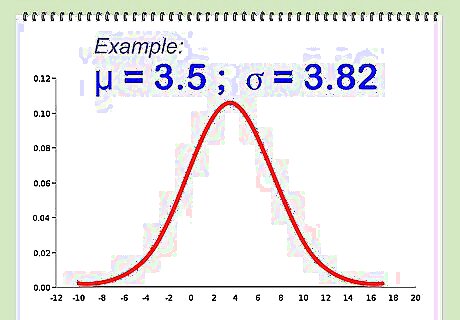
Use the normal distribution with the above mean and standard deviation as an approximation of the sum of the dice.