views
Using a Spreadsheet
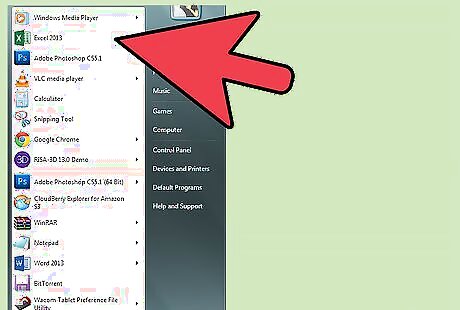
Launch your preferred spreadsheet. This could be Microsoft Excel, Zoho Sheets, Google Docs Sheet or another spreadsheet application. Create labels for the variables relating to your account in cells A1 down through A5 as follows: Balance, Interest Rate, Periods, Additional Deposits and Future Value.
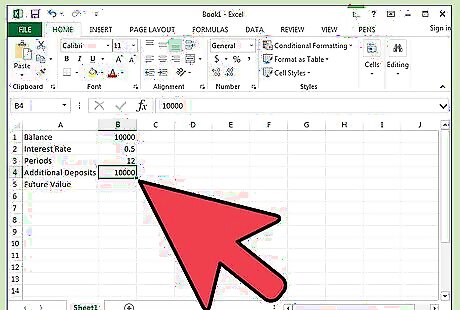
Enter the details for your current savings plan. Enter these numbers in cells from B1 down through B4. This includes your current balance, interest rate earned, number of months, and any additional deposits you plan to make over time. Make sure you know the compound period of your interest rate — not all interest is compounded on a monthly basis and this number will make a difference on the outcome. The compounding period could be yearly, monthly, quarterly — check with your financial institution to find out the period. If the compound period is once a month, then you will divide your annual interest rate by 12 to arrive at a monthly interest rate. You will want to enter the number of periods as months, not years. In addition, be sure input the interest rate as a decimal instead of as a percentage. Convert this number by dividing by 100. For example, 6% would be entered as 6%/100, or 0.06. This would then by converted to a monthly rate by dividing by 12, to get 0.06/12, or 0.005.
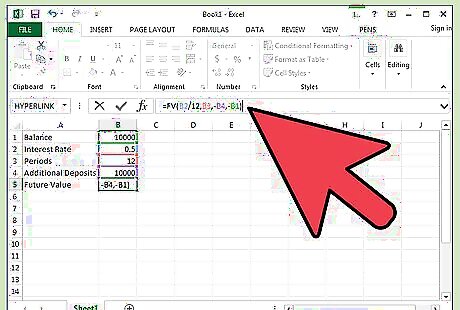
Create a formula in cell B5. This will calculate the future value of your savings. Type "=FV(B2,B3,-B4,-B1)" in the address bar. Or you can click the function button (labeled "fx") and choose the Future Value formula to create the formula. For this example, assume that you have $500 as a beginning balance, that your savings account earns 2 percent interest each month, that you will not be depositing additional money each month and that you want to see the result after five years.
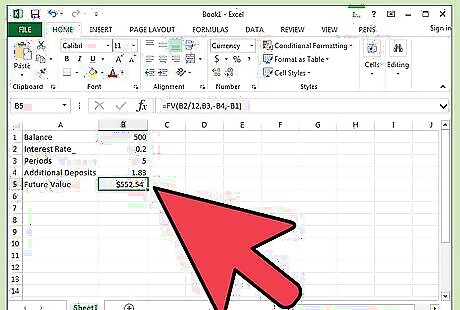
Review the formula result. Using the example variables, this account should total $552.54 after five years. In other words, at 2 percent interest, you will earn $52.54 after five years on savings of $500.
Changing Variables for Future Results
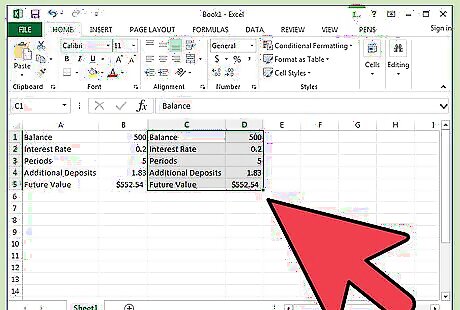
Predict results by changing the variables. Copy cells A1 through B5 and paste in cells C1 through D5. This will copy the formulas you previously entered.
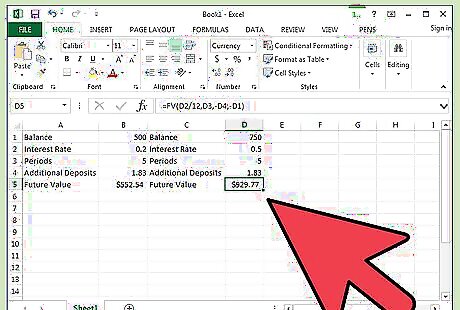
Change the variables in rows D1 down through D4. You can examine other scenarios such as a lower interest rate, a longer period, or an additional monthly payment. Simply enter a new value for each variable, or change them all at once.
Compare the results. By simply increasing the interest rate, number of years, or payment, you can see drastically higher future values for your investments. Play around with the numbers and see how an extra $20 per month can affect your account value over 10 or 20 years.
Use an amortization table. You can calculate the future value of an account with a varying interest rate and additional monthly payments using an amortization table. These can be found online by searching for "compound interest amortization tables."
Solving for Accumulated Saving Manually

Gather the details of your savings plan. You will need the beginning balance, fixed interest rate and the period for which you would like to calculate. Assume you will not be making any additional deposits.
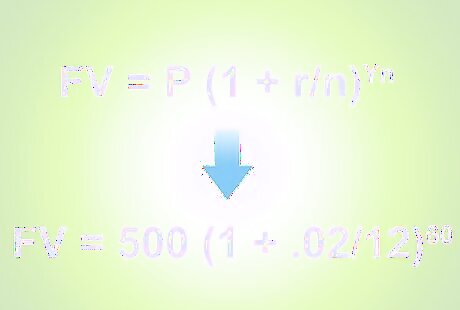
Enter data into the formula. Replace the variables in the formula F V = P ( 1 + i c ) n ∗ c {\displaystyle FV=P(1+{\frac {i}{c}})^{n*c}} FV=P(1+{\frac {i}{c}})^{{n*c}} with your actual details. Here is what the variables represent: FV represents the future value of your account Replace "P" with the amount of your beginning balance. Replace "r" with the annual interest rate, expressed as a decimal Replace "c"with the number of times your interest is compounded each year. Replace "n" with the the number of years you are measuring growth over.

Use the "PEMDAS" rule. This is used to calculate first the part of the equation in parentheses, then the exponents and finally the multiplication."PEMDAS" is an acronym for "parentheses, exponents, multiplication, division, addition and subtraction" and provides the order that mathematical operations should take place. Assume your account details include a $500 starting balance in an account bearing 2 percent interest, compounded monthly. Assume, also, that you are looking for the future value of your account after five years. Your completed equation would look as follows: F V = $ 500 ( 1 + 0.02 12 ) 5 ∗ 12 {\displaystyle FV=\$500(1+{\frac {0.02}{12}})^{5*12}} FV=\$500(1+{\frac {0.02}{12}})^{{5*12}} Solving for the multiplication and division within the parentheses first, we get: F V = $ 500 ( 1 + 0.00167 ) 24 {\displaystyle FV=\$500(1+0.00167)^{24}} FV=\$500(1+0.00167)^{{24}} Next, solve the addition within the parentheses to get: F V = $ 500 ( 1.00167 ) 24 {\displaystyle FV=\$500(1.00167)^{24}} FV=\$500(1.00167)^{{24}} Raise the number within parentheses to the exponent: F V = $ 500 ( 1.105 ) {\displaystyle FV=\$500(1.105)} FV=\$500(1.105) This can be done on a calculator by entering the number in parentheses, pressing the x y {\displaystyle x^{y}} x^{y} button, then entering the exponent and pressing enter. Multiply the two remaining numbers to get your accumulated savings amount: F V = $ 552.50 {\displaystyle FV=\$552.50} FV=\$552.50

















Comments
0 comment