Calculate the Spring Constant Using Hooke’s Law: Formula, Examples, and Practice Problems

• Use the formula ${\displaystyle k={\frac {F}{x}}}$ to find the spring constant for an ideal spring.
• Express Hooke's Law mathematically with the equation ${\displaystyle F=-kx}$.
• Display the spring constant on a graph as the slope of a straight line since the relationship between force and distance is linear.

What is the formula for the spring constant?

The formula to find the spring constant is k = F x {\displaystyle k={\frac {F}{x}}} {\displaystyle k={\frac {F}{x}}}. When you push or pull a spring, it bounces back to its original rest position or equilibrium. The spring constant, measured in N / m {\displaystyle N/m} {\displaystyle N/m} (Newton/meters or Newtons per meter), tells you the proportional force exerted by the spring that causes it to bounce back. These variables have a linear relationship: k {\displaystyle k} k: Spring constant F {\displaystyle F} F: Force (the force applied to the spring) x {\displaystyle x} x: Distance the spring is compressed or stretched away from its equilibrium or rest position

What is Hooke's Law?

Hooke's law states that when a force compresses or stretches a spring, it will bounce back to its rest position with an equal and opposite force. That bounce-back or restoring force is known as the spring constant because it's always the same for a given spring. You can express this law mathematically with the equation F = − k x {\displaystyle F=-kx} {\displaystyle F=-kx}. The negative symbol indicates that the force of the spring constant is in the opposite direction of the force applied to the spring. It does not indicate that the value is negative. Hooke's law is actually pretty limited. It only applies to perfectly elastic materials within their elastic limit—stretch something too far and it'll break or stay stretched out. Hooke's law is based on Newton's third law of motion, which states that for every action there is an equal and opposite reaction.

How does spring length affect the spring constant?

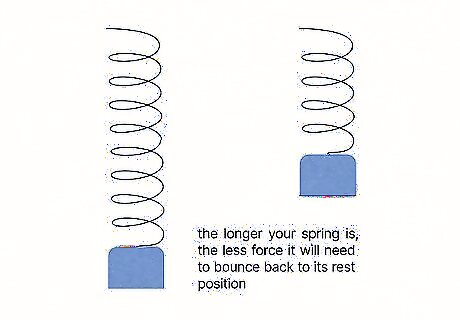
The spring constant is inversely related to the spring's equilibrium length. This means that the longer your spring is, the less force it will need to bounce back to its rest position or equilibrium. A shorter spring, on the other hand, requires more force to bounce back. This makes sense if you think of springs you've encountered—the spring constant measures the stiffness of a spring, and short springs tend to be stiffer than long springs. For example, if you cut a spring in half, its spring constant will double. If you doubled the length of the spring, on the other hand, its spring constant would be half what it was. This also means that when you apply the same force to a longer spring as a shorter spring, the longer spring will stretch further than the shorter spring.

Practice Problems

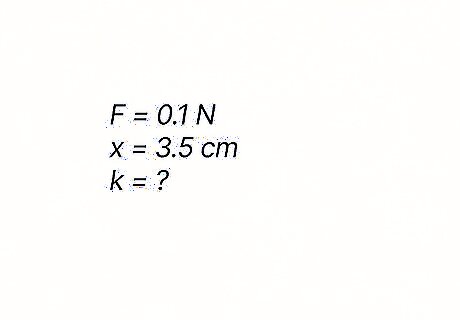
Find the spring constant of a stretched spring that supports 0.1 N {\displaystyle 0.1N} {\displaystyle 0.1N} of weight if the spring stretches another 3.5 c m {\displaystyle 3.5cm} {\displaystyle 3.5cm} when 0.1 N {\displaystyle 0.1N} {\displaystyle 0.1N} is added to it. Hint: Since the spring constant is measured in N / m {\displaystyle N/m} {\displaystyle N/m}, convert 3.5 c m {\displaystyle 3.5cm} {\displaystyle 3.5cm} to 0.035 m {\displaystyle 0.035m} {\displaystyle 0.035m}.

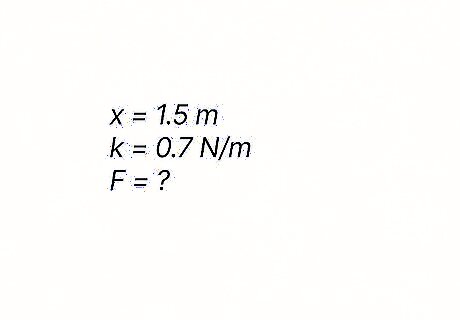
What force is required to stretch a spring 1.5 m {\displaystyle 1.5m} {\displaystyle 1.5m} if the spring has a spring constant of 0.7 N / m {\displaystyle 0.7N/m} {\displaystyle 0.7N/m}? Hint: Use the equation for Hooke's Law without the negative symbol, which doesn't have a mathematical function: F = k x {\displaystyle F=kx} {\displaystyle F=kx}.

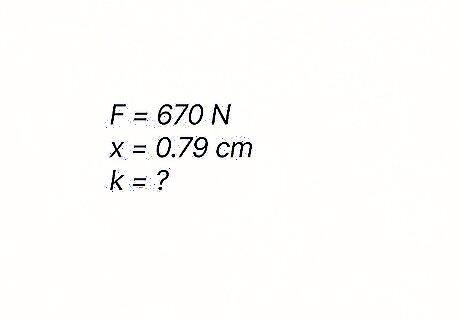
If a person who weighs 670 N {\displaystyle 670N} {\displaystyle 670N} steps on a scale, the scale's spring compresses by 0.79 c m {\displaystyle 0.79cm} {\displaystyle 0.79cm}. What is the spring constant of the scale's spring? Hint: The person's weight is equivalent to the force applied to the spring.

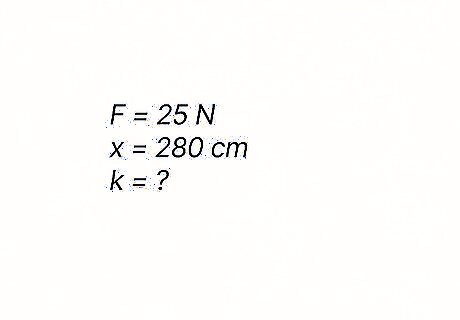
What is the spring constant of a spring if it stretches 280 c m {\displaystyle 280cm} {\displaystyle 280cm} when a 25 N {\displaystyle 25N} {\displaystyle 25N} force is applied? Hint: Remember to convert the c m {\displaystyle cm} cm to m {\displaystyle m} m since the spring constant is measured in N / m {\displaystyle N/m} {\displaystyle N/m}.

Solutions to Practice Problems

The spring constant is 2.85 N / m {\displaystyle 2.85N/m} {\displaystyle 2.85N/m}. You aren't given the distance the spring is stretched when the first 0.1 N {\displaystyle 0.1N} {\displaystyle 0.1N} is added to it, but that doesn't matter because the spring constant is always the same. Plug the values for the second weight into the formula to find the spring constant: The formula to find the spring constant is k = F x {\displaystyle k={\frac {F}{x}}} {\displaystyle k={\frac {F}{x}}}. Here, the force is 0.1 N {\displaystyle 0.1N} {\displaystyle 0.1N} and the distance the spring stretches when that force is added is 0.035 m {\displaystyle 0.035m} {\displaystyle 0.035m}, so your equation is k = 0.1 0.035 {\displaystyle k={\frac {0.1}{0.035}}} {\displaystyle k={\frac {0.1}{0.035}}}. Divide 0.1 {\displaystyle 0.1} {\displaystyle 0.1} by 0.035 {\displaystyle 0.035} {\displaystyle 0.035}, then round to get your answer of 2.85 N / m {\displaystyle 2.85N/m} {\displaystyle 2.85N/m}. Why not 0.2 N {\displaystyle 0.2N} {\displaystyle 0.2N}? Because you don't know the distance the string stretched when the first weight was applied. You only know the additional distance it stretched when the second weight was applied.

The force applied is 1.05 N {\displaystyle 1.05N} {\displaystyle 1.05N}. Plug the values you were given into the equation for Hooke's Law and you get F = ( 0.7 ) ( 1.5 ) {\displaystyle F=(0.7)(1.5)} {\displaystyle F=(0.7)(1.5)}. Then, you simply multiply to find the answer.

The spring constant of the scale's spring is 84 , 810 N / m {\displaystyle 84,810N/m} {\displaystyle 84,810N/m}. First, convert c m {\displaystyle cm} cm to m {\displaystyle m} m, since the spring constant is measured in N / m {\displaystyle N/m} {\displaystyle N/m}. Then, plug the values into your equation to find the spring constant: k = F x {\displaystyle k={\frac {F}{x}}} {\displaystyle k={\frac {F}{x}}} k = 670 0.0079 {\displaystyle k={\frac {670}{0.0079}}} {\displaystyle k={\frac {670}{0.0079}}} k = 84 , 810 N / m {\displaystyle k=84,810N/m} {\displaystyle k=84,810N/m}

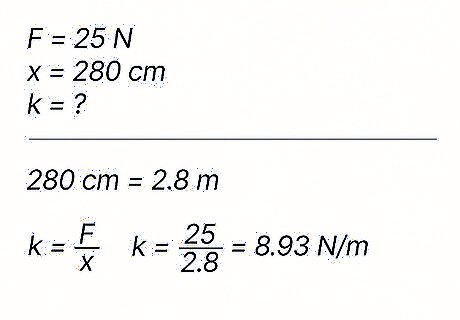
The spring constant is 8.93 N / m {\displaystyle 8.93N/m} {\displaystyle 8.93N/m}. Start by converting 280 c m {\displaystyle 280cm} {\displaystyle 280cm} to 2.8 m {\displaystyle 2.8m} {\displaystyle 2.8m}. Then, since you're asked to find the spring constant, use the formula k = F x {\displaystyle k={\frac {F}{x}}} {\displaystyle k={\frac {F}{x}}}: k = 25 2.8 {\displaystyle k={\frac {25}{2.8}}} {\displaystyle k={\frac {25}{2.8}}} k = 8.93 N / m {\displaystyle k=8.93N/m} {\displaystyle k=8.93N/m}

How do I display Hooke's Law on a graph?

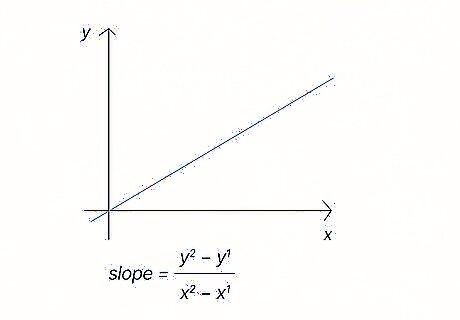
Hooke's Law describes a directly proportional linear relationship between the force exerted on a spring and the distance it moves. Within this relationship, the spring constant is the slope of the line on a graph. The distance values are the x {\displaystyle x} x coordinates and the applied force values are the y {\displaystyle y} ycoordinates. If you're given a line that represents a spring that obeys Hooke's Law (also called an ideal spring), you can find the spring constant by finding the slope of the line using the basic slope formula y 2 − y 1 x 2 − x 1 {\displaystyle {\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}} {\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}. A line with a spring constant as a slope will always cross through the origin of the graph.