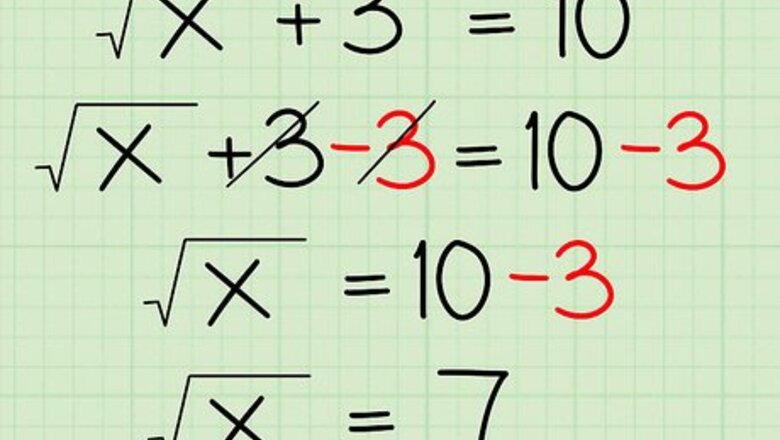
views
x
{\displaystyle {\sqrt {x}}}
. The root is typically a square root, but it can be a cube root or other roots -- it won't change how you solve the equation. If you remember that the opposite of a radical is an exponent (for example, that
x
2
=
x
{\displaystyle {\sqrt {x}}^{2}=x}
), then solving radical equations is actually pretty easy.
Solving Equations with One Radical
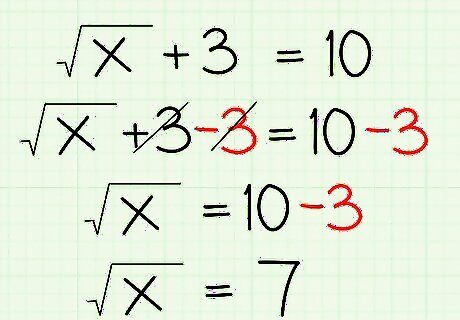
Isolate the variable and radical on one side of the equation. This is just like solving for any other algebraic equation. Combine like terms and add/subtract numbers so that your variable and radical stand alone. If it helps, treat the x {\displaystyle {\sqrt {x}}} {\sqrt {x}} like a normal "x" in any other problem, and solve for that. For example, with the problem x + 3 = 10 {\displaystyle {\sqrt {x}}+3=10} {\sqrt {x}}+3=10: Isolate x {\displaystyle {\sqrt {x}}} {\sqrt {x}}: x + 3 = 10 {\displaystyle {\sqrt {x}}+3=10} {\sqrt {x}}+3=10 Subtract 3 from both sides: x + 3 − 3 = 10 − 3 {\displaystyle {\sqrt {x}}+3-3=10-3} {\sqrt {x}}+3-3=10-3 Simplify both sides: x = 7 {\displaystyle {\sqrt {x}}=7} {\sqrt {x}}=7
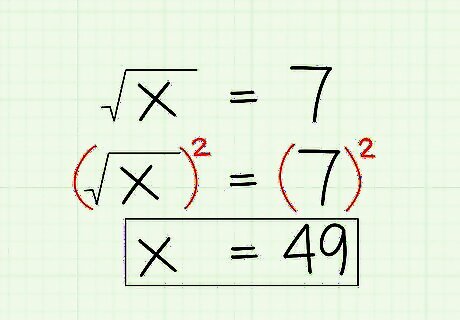
Square both sides of the equation to remove the radical. All you have to do to undo a radical is square it. Because you need the equation to stay balanced, you square both sides, just like you added or subtracted from both sides earlier. So, for the example: Isolate x {\displaystyle {\sqrt {x}}} {\sqrt {x}}: x = 7 {\displaystyle {\sqrt {x}}=7} {\sqrt {x}}=7 Square both sides: ( x ) 2 = ( 7 ) 2 {\displaystyle ({\sqrt {x}})^{2}=(7)^{2}} ({\sqrt {x}})^{2}=(7)^{2} Final answer: x = 49 {\displaystyle x=49} x=49
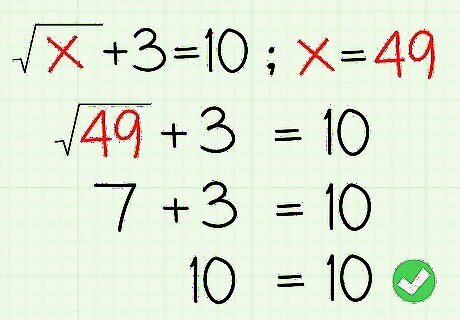
Check your answers in the original problem. When solving radical equations, you can get answers that don't actually fit the problem. You must always check your solutions to make sure you have all real answers. To check an answer, simply plug in each answer for "x" in the original equation: Original Equation: x + 3 = 10 {\displaystyle {\sqrt {x}}+3=10} {\sqrt {x}}+3=10 Substitute 49 for x: 49 + 3 = 10 {\displaystyle {\sqrt {49}}+3=10} {\sqrt {49}}+3=10 Solve: 7 + 3 = 10 {\displaystyle 7+3=10} 7+3=10 Our solution is valid: 10 = 10 {\displaystyle 10=10} 10=10

Use the same technique for more complicated roots, not just squares. This same strategy works no matter what the root, like x 3 − 1 = 3 {\displaystyle {\sqrt[{3}]{x}}-1=3} {\sqrt[ {3}]{x}}-1=3. You just need to raise both sides to the same power as the root. So, for this example: Isolate x 3 {\displaystyle {\sqrt[{3}]{x}}} {\sqrt[ {3}]{x}}: x 3 − 1 = 3 {\displaystyle {\sqrt[{3}]{x}}-1=3} {\sqrt[ {3}]{x}}-1=3 Add 1 to both sides: x 3 − 1 + 1 = 3 + 1 {\displaystyle {\sqrt[{3}]{x}}-1+1=3+1} {\sqrt[ {3}]{x}}-1+1=3+1 Simplify both sides: x 3 = 4 {\displaystyle {\sqrt[{3}]{x}}=4} {\sqrt[ {3}]{x}}=4 Cube both sides: ( x 3 ) 3 = ( 4 ) 3 {\displaystyle ({\sqrt[{3}]{x}})^{3}=(4)^{3}} ({\sqrt[ {3}]{x}})^{3}=(4)^{3} Final Answer: 64 Check Solution: 64 3 − 1 = 4 − 1 = 3 {\displaystyle {\sqrt[{3}]{64}}-1=4-1=3} {\sqrt[ {3}]{64}}-1=4-1=3
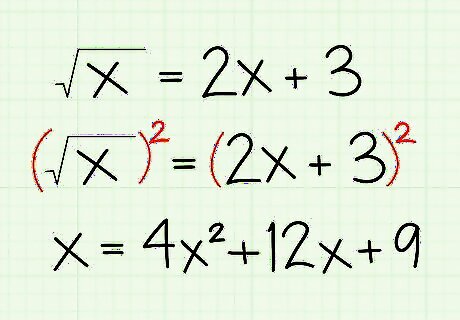
Remember to square both sides of the equation, not just the terms. When removing the radical, you square both sides of the equation. If you have multiple terms, such as the equation x = 2 x + 3 {\displaystyle {\sqrt {x}}=2x+3} {\sqrt {x}}=2x+3, you must square the entire side, not the individual terms ( 2 x 2 {\displaystyle 2x^{2}} 2x^{2} and 3 2 {\displaystyle 3^{2}} 3^{2} are both incorrect). Before solving for x in the example, then: Original Equation: x = 2 x + 3 {\displaystyle {\sqrt {x}}=2x+3} {\sqrt {x}}=2x+3 Square both sides: ( x ) 2 = ( 2 x + 3 ) 2 {\displaystyle ({\sqrt {x}})^{2}=(2x+3)^{2}} ({\sqrt {x}})^{2}=(2x+3)^{2} Expand Expressions: x = 4 x 2 + 12 x + 9 {\displaystyle x=4x^{2}+12x+9} x=4x^{2}+12x+9 The expression above was expanded through Polynomial Multiplication. If you're confused how it was done, you can review the process here.
Solving Equations with Multiple Radicals
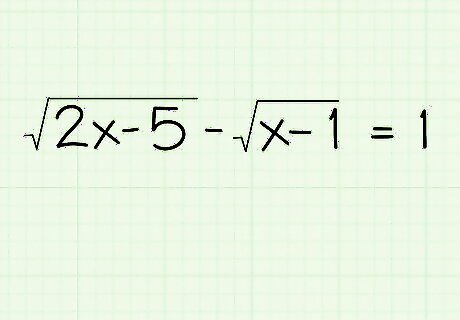
Use the isolation strategy, with just a few new tricks, to solve complicated radical equations. If you've got two radicals in your equation, don't panic. The basics of solving radical equations are still the same. You want to get the variables by themselves, remove the radicals one at a time, solve the leftover equation, and check all known solutions. For this example, solve the radical equation 2 x − 5 − x − 1 = 1 {\displaystyle {\sqrt {2x-5}}-{\sqrt {x-1}}=1} {\sqrt {2x-5}}-{\sqrt {x-1}}=1 You frequently end up with quadratic equations when working with radicals. Review how to solve them if you are unsure.
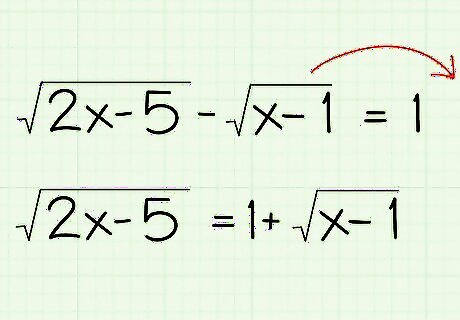
Isolate one of the variables under the radical. Get one of the variables alone, like you would normally. Ignore the other for now. For the example, simply add x − 1 {\displaystyle {\sqrt {x-1}}} {\sqrt {x-1}} to each side: Original Problem: 2 x − 5 − x − 1 = 1 {\displaystyle {\sqrt {2x-5}}-{\sqrt {x-1}}=1} {\sqrt {2x-5}}-{\sqrt {x-1}}=1 Isolate one radical: 2 x − 5 − x − 1 + x − 1 = 1 + x − 1 {\displaystyle {\sqrt {2x-5}}-{\sqrt {x-1}}+{\sqrt {x-1}}=1+{\sqrt {x-1}}} {\sqrt {2x-5}}-{\sqrt {x-1}}+{\sqrt {x-1}}=1+{\sqrt {x-1}} 2 x − 5 = 1 + x − 1 {\displaystyle {\sqrt {2x-5}}=1+{\sqrt {x-1}}} {\sqrt {2x-5}}=1+{\sqrt {x-1}}
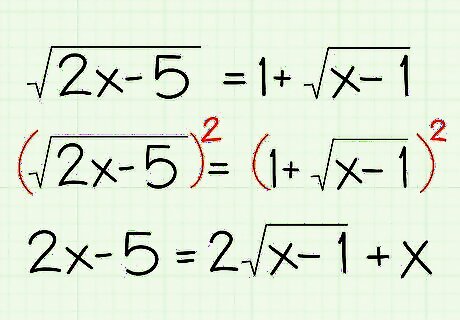
Square both sides of the equation. Again, there is nothing here that you haven't done with simpler equations. Square both sides to remove the radical on the left. Isolated radical: 2 x − 5 = 1 + x − 1 {\displaystyle {\sqrt {2x-5}}=1+{\sqrt {x-1}}} {\sqrt {2x-5}}=1+{\sqrt {x-1}} Square both sides: ( 2 x − 5 ) 2 = ( 1 + x − 1 ) 2 {\displaystyle ({\sqrt {2x-5}})^{2}=(1+{\sqrt {x-1}})^{2}} ({\sqrt {2x-5}})^{2}=(1+{\sqrt {x-1}})^{2} Expand: 2 x − 5 = 1 + 2 x − 1 + ( x − 1 ) {\displaystyle 2x-5=1+2{\sqrt {x-1}}+(x-1)} 2x-5=1+2{\sqrt {x-1}}+(x-1) Simplify: 2 x − 5 = 2 x − 1 + x {\displaystyle 2x-5=2{\sqrt {x-1}}+x} 2x-5=2{\sqrt {x-1}}+x

Isolate the other square root. You've got one of your radical signs gone -- it is time to get rid of the second. Just go through the same motions as the first time, isolating the side with the radical. Simplified equation: 2 x − 5 = 2 x − 1 + x {\displaystyle 2x-5=2{\sqrt {x-1}}+x} 2x-5=2{\sqrt {x-1}}+x Isolate radical: 2 x − 5 − x = 2 x − 1 + x − x {\displaystyle 2x-5-x=2{\sqrt {x-1}}+x-x} 2x-5-x=2{\sqrt {x-1}}+x-x x − 5 2 = 2 x − 1 2 {\displaystyle {\frac {x-5}{2}}={\frac {2{\sqrt {x-1}}}{2}}} {\frac {x-5}{2}}={\frac {2{\sqrt {x-1}}}{2}} x − 5 2 = x − 1 {\displaystyle {\frac {x-5}{2}}={\sqrt {x-1}}} {\frac {x-5}{2}}={\sqrt {x-1}}
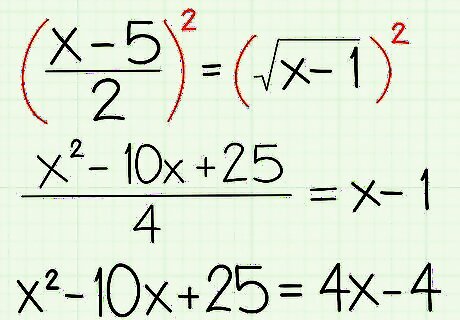
Square both sides. Again, you can do this with any root -- if you have a cube root, you would cube both sides, if it is the 4th root, you'd raise both sides to the 4th power, etc. Your goal is simply to undo the radical. Isolated Final Radical: x − 5 2 = x − 1 {\displaystyle {\frac {x-5}{2}}={\sqrt {x-1}}} {\frac {x-5}{2}}={\sqrt {x-1}} Square both sides: ( x − 5 2 ) 2 = ( x − 1 ) 2 {\displaystyle ({\frac {x-5}{2}})^{2}=({\sqrt {x-1}})^{2}} ({\frac {x-5}{2}})^{2}=({\sqrt {x-1}})^{2} Expand both sides: ( x 2 − 10 x + 25 ) 4 = x − 1 {\displaystyle {\frac {(x^{2}-10x+25)}{4}}=x-1} {\frac {(x^{2}-10x+25)}{4}}=x-1 Simplify: x 2 − 10 x + 25 = 4 x − 1 {\displaystyle x^{2}-10x+25=4x-1} x^{2}-10x+25=4x-1
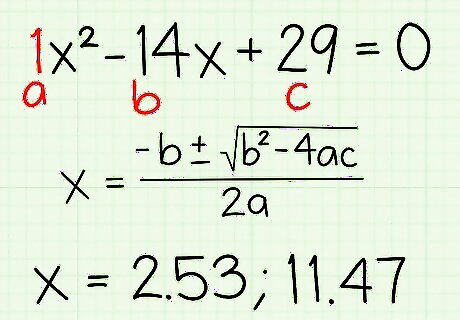
Solve for "x" once all the radicals are gone. Theoretically, you could keep doing this no matter how many radicals you have, though you can see how complicated things would quickly get. Once you've got both radicals gone, it is time to use your algebra skills solve for x. In this example, x 2 − 10 x + 25 = 4 x − 4 {\displaystyle x^{2}-10x+25=4x-4} x^{2}-10x+25=4x-4, you'll need to use the quadratic equation. You could also graph both sides of the equation and see where they meet. Using the quadratic equation, you only get two possible answers: 2.53 and 11.47.

Check all possible solutions to get the right answer. Remember, not all answers you find are going to be correct. You need to plug them back in to check them. If an answer isn't part of the solution you can feel free to toss it out, though some teachers want you to show that you found and discarded the answer in your work. Check 2.53: 2 ( 2.53 ) − 5 − ( 2.53 ) − 1 = 1 {\displaystyle {\sqrt {2(2.53)-5}}-{\sqrt {(2.53)-1}}=1} {\sqrt {2(2.53)-5}}-{\sqrt {(2.53)-1}}=1 Answer does not check out, x = 2.53 {\displaystyle x=2.53} x=2.53 is not a solution. Check 11.74: 2 x − 5 − x − 1 = 1 {\displaystyle {\sqrt {2x-5}}-{\sqrt {x-1}}=1} {\sqrt {2x-5}}-{\sqrt {x-1}}=1 Answer checks out, x = 11.74 {\displaystyle x=11.74} x=11.74 is a solution. The final answer to the problem 2 x − 5 − x − 1 = 1 {\displaystyle {\sqrt {2x-5}}-{\sqrt {x-1}}=1} {\sqrt {2x-5}}-{\sqrt {x-1}}=1 is 11.74.


















Comments
0 comment