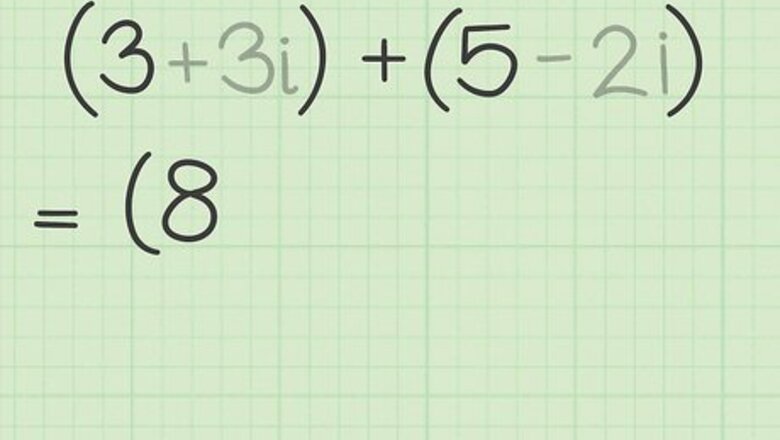
views
i
=
−
1
{\displaystyle i={\sqrt {-1}}}
. A complex number, then, is made of a real number and some multiple of i. Some sample complex numbers are 3+2i, 4-i, or 18+5i. Complex numbers, as any other numbers, can be added, subtracted, multiplied or divided, and then those expressions can be simplified. You need to apply special rules to simplify these expressions with complex numbers.
Adding or Subtracting Complex Numbers
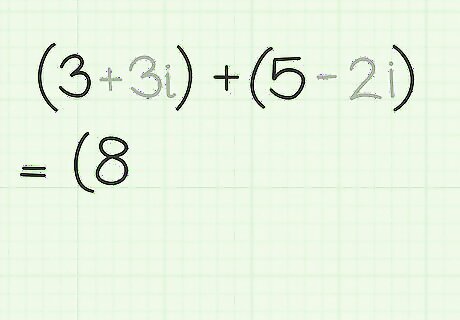
Add the real portions together. Recognize that addition and subtraction are really the same process. Subtraction is nothing more than adding a negative number. Therefore, addition and subtraction are treated as versions of the same process. To add two or more complex numbers, first just add the real portions of the numbers together. For example, to simplify the sum of (a+bi) and (c+di), first identify that a and c are the real number portions, and add them together. Symbolically, this will be (a+c). Using actual numbers instead of variables, consider the example of (3+3i) + (5-2i). The real portion of the first number is 3, and the real portion of the second complex number is 5. Add these together to get 3+5=8. The real portion of the simplified complex number will be 8.
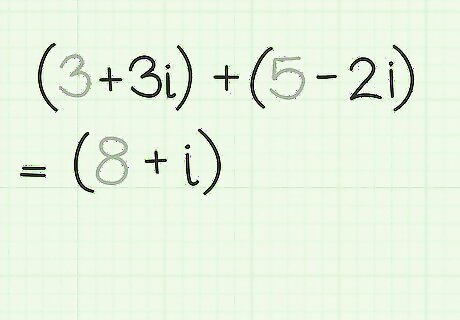
Add the imaginary portions together. In a separate operation, identify the imaginary portions of each complex number and add them together. For the algebraic example of (a+bi) plus (c+di), the imaginary portions are b and d. Adding these together algebraically gives the result (b+d)i. Using the numerical example of (3+3i) + (5-2i), the imaginary portions of the two complex numbers are 3i and -2i. Adding these gives the result of 1i, which can also be written just as i.
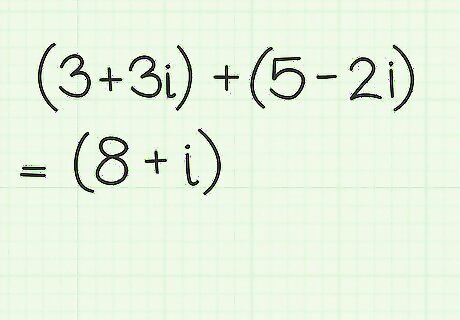
Combine the two parts to form the simplified answer. To find the final simplified version of the sum, put the real part and the imaginary part back together. The result is the simplified sum of the complex numbers. The sum of (a+bi) and (c+di) is written as (a+c) + (b+d)i. Applying the numerical example, the sum of (3+3i) + (5-2i) is 8+i.
Multiplying Complex Numbers
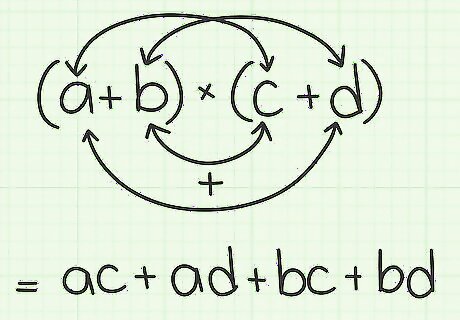
Remember the F-O-I-L rule. Looking at a complex number (a+bi) should remind you of binomials from Algebra or Algebra 2. Remember that to multiply binomials, you need to multiply each term of the first binomial by each term of the second. A shorthand version for doing this, is the F-O-I-L rule, which stands for “First, Outer, Inner, Last.” For an example of (a+b)(c+d), apply this rule as follows: First. The F in FOIL means that you multiply the first term of the first binomial by the first term of the second binomial. For the sample, this would be a*c. Outer. The O in FOIL tells you to multiply the “outer” terms. These are the first term of the first binomial and the second term of the second binomial. For the sample, this would be a*d. Inner. The I in FOIL means to multiply the “inner” terms. These would be the two terms that appear in the middle, which are the second term of the first binomial and the first term of the second binomial. In the given example, the inner terms are b*c. Last. The L in FOIL represents the last terms of each binomial. For the sample expression, this would be b*d. Finally, add all four products together. The result for the sample binomial multiplication of (a+b)(c+d) is ac+ad+bc+bd.
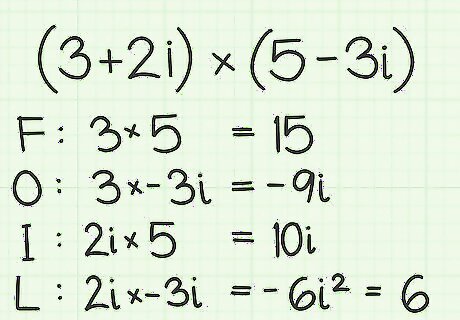
Apply the FOIL rule to complex number multiplication. To multiply two complex numbers, set them up as the product of two binomials and apply the FOIL rule. For example, the product of the two complex numbers (3+2i)*(5-3i) works as follows: First. The product of the first terms is 3*5=15. Outer. The product of the outer terms is 3*(-3i). This product is -9i. Inner. The product of the two inner terms is 2i*5. This product is 10i. Last. The product of the last terms is (2i)*(-3i). This product is -6i. Recognize that i equals -1, so the value of -6i is -6*-1, which is 6.
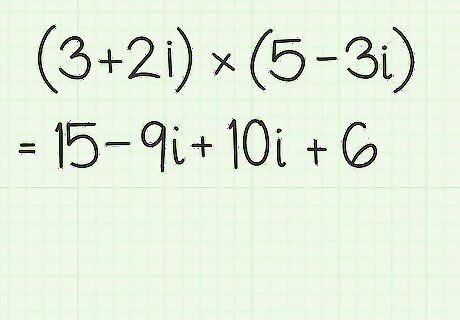
Combine the terms. After applying the FOIL rule and finding the four independent products, combine them together to find the result of the multiplication. For the sample (3+2i)*(5-3i), the parts combine to give 15-9i+10i+6.
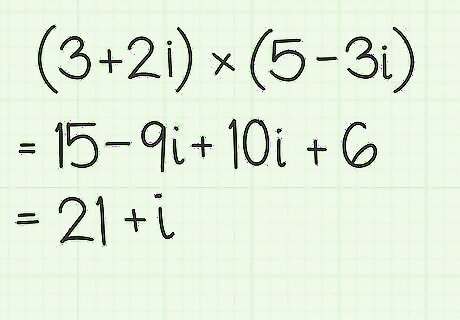
Simplify by combining like terms. The result of the FOIL rule multiplication should yield two real number terms and two imaginary number terms. Simplify the result by combining like terms together. For the sample 15-9i+10i+6, you can add the 15 and 6 together and add the -9i and the 10i together. The result will be 21+i.
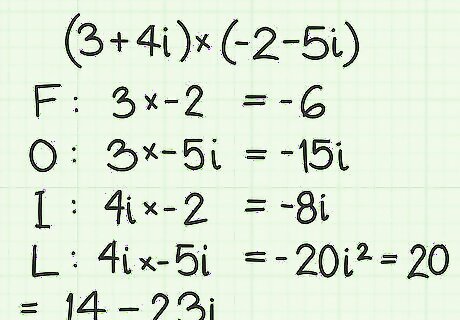
Work through one more example. Find the product of the two complex numbers (3+4i)(-2-5i). The steps for this multiplication are: (3)(-2)=-6 (First) (3)(-5i)=-15i (Outer) (4i)(-2)=-8i (Inner) (4i)(-5i)=-20i=(-20)(-1)=20 (Lasts) -6-15i-8i+20 = 14-23i (Combine terms and simplify)
Dividing Complex Numbers
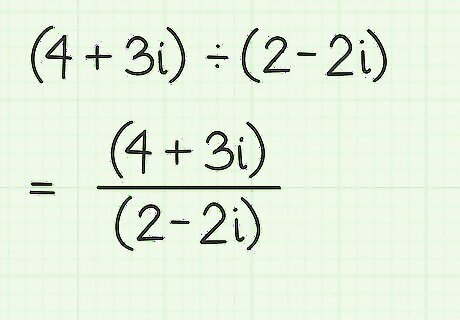
Write the division of two complex numbers as a fraction. When you want to divide two complex numbers, set up the problem as a fraction. For example, to find the quotient of (4+3i) divided by (2-2i), set up the problem as follows: ( 4 + 3 i ) ( 2 − 2 i ) {\displaystyle {\frac {(4+3i)}{(2-2i)}}} {\frac {(4+3i)}{(2-2i)}}
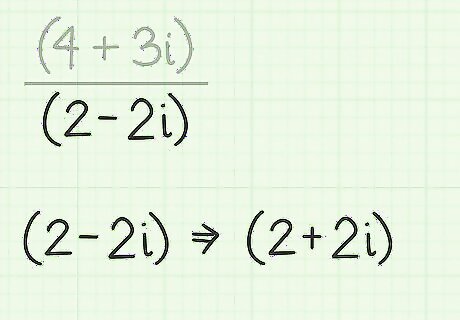
Find the conjugate of the denominator. The conjugate of a complex number is a useful tool. It is simply created by changing the sign in the middle of the complex number. Thus, the conjugate of (a+bi) is (a-bi). The conjugate of (2-3i) is (2+3i).
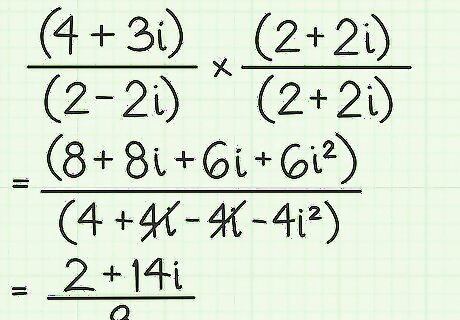
Multiply the numerator and denominator by the conjugate of the denominator. Whenever you multiply by a fraction whose numerator and denominator are identical, the value is just 1. This is a useful tool for simplifying complex numbers, particularly for division problems. Thus, set up the example ( 4 + 3 i ) ( 2 − 2 i ) {\displaystyle {\frac {(4+3i)}{(2-2i)}}} {\frac {(4+3i)}{(2-2i)}} as follows: ( 4 + 3 i ) ( 2 − 2 i ) ∗ ( 2 + 2 i ) ( 2 + 2 i ) {\displaystyle {\frac {(4+3i)}{(2-2i)}}*{\frac {(2+2i)}{(2+2i)}}} {\frac {(4+3i)}{(2-2i)}}*{\frac {(2+2i)}{(2+2i)}} Then multiply the numerator and denominator and simplify as follows: ( 4 + 3 i ) ( 2 − 2 i ) ∗ ( 2 + 2 i ) ( 2 + 2 i ) {\displaystyle {\frac {(4+3i)}{(2-2i)}}*{\frac {(2+2i)}{(2+2i)}}} {\frac {(4+3i)}{(2-2i)}}*{\frac {(2+2i)}{(2+2i)}} 8 + 8 i + 6 i + 6 i 2 4 + 4 i − 4 i − 4 i 2 {\displaystyle {\frac {8+8i+6i+6i^{2}}{4+4i-4i-4i^{2}}}} {\frac {8+8i+6i+6i^{2}}{4+4i-4i-4i^{2}}} 8 + 14 i + 6 ( − 1 ) 4 − 4 ( − 1 ) {\displaystyle {\frac {8+14i+6(-1)}{4-4(-1)}}} {\frac {8+14i+6(-1)}{4-4(-1)}} 8 + 14 i − 6 4 + 4 {\displaystyle {\frac {8+14i-6}{4+4}}} {\frac {8+14i-6}{4+4}} 2 + 14 i 8 {\displaystyle {\frac {2+14i}{8}}} {\frac {2+14i}{8}} Notice in the second step above, the denominator contains the terms + 4 i {\displaystyle +4i} +4i and − 4 i {\displaystyle -4i} -4i. These will cancel each other out. This will always happen as a result of multiplying by the conjugate. The imaginary terms of the denominator should always cancel and disappear.
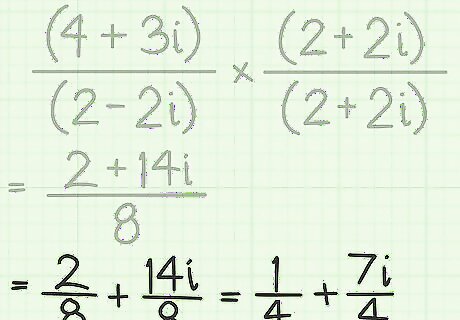
Return to complex number format. Recognize that the single denominator applies equally to both portions of the numerator. Split the numerator apart to create a standard complex number. 2 + 14 i 8 = 2 8 + 14 i 8 = 1 4 + 7 i 4 {\displaystyle {\frac {2+14i}{8}}={\frac {2}{8}}+{\frac {14i}{8}}={\frac {1}{4}}+{\frac {7i}{4}}} {\frac {2+14i}{8}}={\frac {2}{8}}+{\frac {14i}{8}}={\frac {1}{4}}+{\frac {7i}{4}}


















Comments
0 comment