How to Memorize the Unit Circle

Remembering the Radians with the ASAP Trick

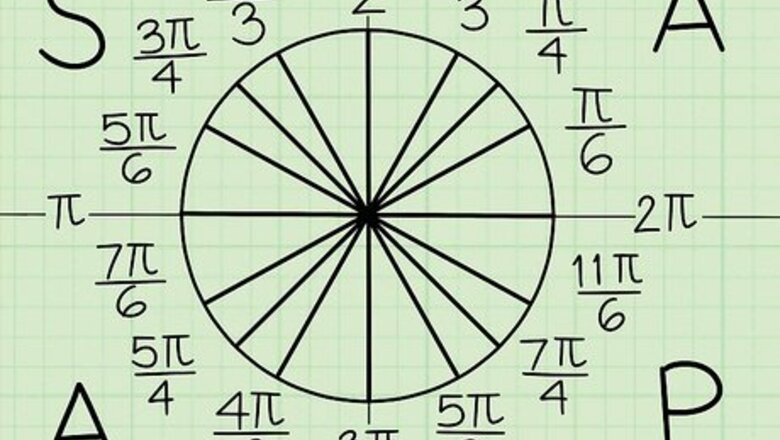
Learn that ASAP means “All, Subtract, Add, Prime.” You can remember it using the acronym “A Student Always Practices.” This handy acronym can help you remember how to find the radians for each angle. Unfortunately, the radians aren’t the same across the different quadrants, though they do share common denominators. That’s because the radians will be in order from 0 to 2????. All - You need to memorize all of the first quadrant radians. Subtract - To get the numerator of each radian in the second quadrant, you subtract 1 from the denominator for the corresponding first quadrant angle. Add - To get the numerator of each radian in the third quadrant, you add 1 to the denominator for the corresponding first quadrant angle. Prime numbers - Each radian in the fourth quadrant starts with a prime number.

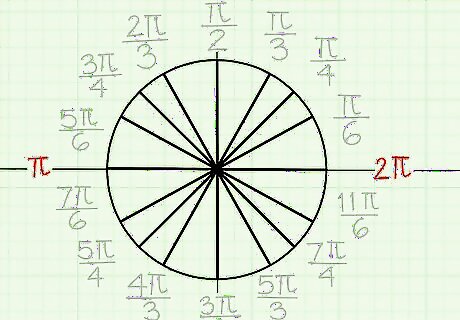
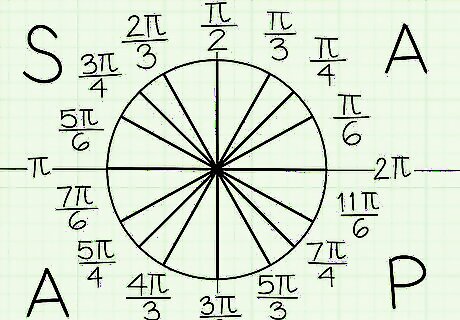
See that the x-axis is not a fraction. It’s helpful to think of your x-axis as a whole number. The positive side is 0 or 2????, while the negative side is 1????. That is because the top part of the circle by itself measures 1????, plus the bottom part of the circle by itself also measures 1????. The negative side of the x-axis is halfway around your circle, while the positive side is both the start and finish of the circle.

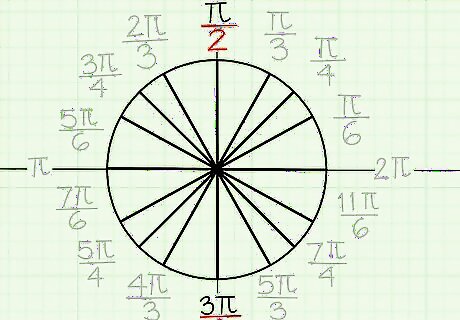
Notice that the y-axis has a denominator of 2. Since the entire top half of the circle measures 1????, it makes sense that the measurement of the positive y-axis would be 1????/2. That’s because the y-axis splits the top part of the circle in half. Similarly, the bottom part of the circle is 3????/2 because the negative y-axis is splitting it in half. If you have trouble remembering that the negative y-axis is 3????/2, you can use the addition addition trick for finding the third quadrant radians.

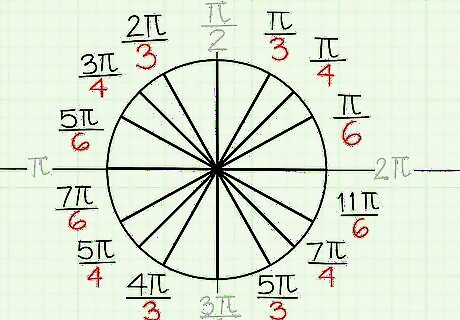
Recognize each quadrant shares the denominators 6, 4, and 3. This makes it easier to memorize the radians. The number 3 is always close to the y-axis, while the number 6 is always close to the x-axis. That might seem tricky, but it helps to remember that the smaller numbers are on top or bottom, while the larger numbers are side to side. Quadrant 1 denominators look like this: 6, 4, 3 Quadrant 2 denominators look like this: 3, 4, 6 Quadrant 3 denominators are in this order: 6, 4, 3 Quadrant 4 denominators are in this order: 3, 4, 6

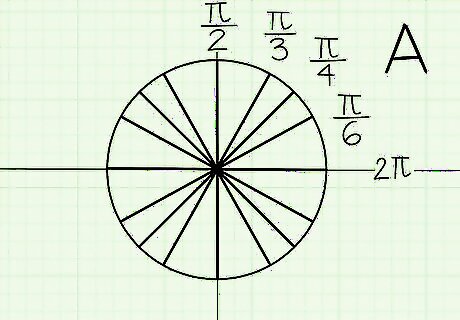
Learn all the radians for the first quadrant angles. A radian is the measure of an angle. Each measurement will be in pi, since a circle’s circumference is based on pi. The radians of a unit circle go from 0 to 2????. Most angles on your circle will be a fraction of pi. Here are the radian measurements for the first quadrant: 0 degree angles have a measurement of 0. A 30 degree angle has a measurement of ????/6. A 45 degree angle has a measurement of ????/4. A 60 degree angle has a measurement of ????/3. A 90 degree angle has a measurement of ????/2.

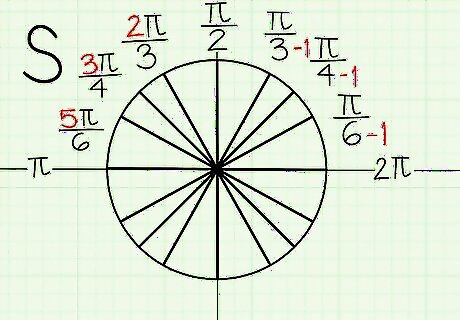
Subtract 1 from the denominator to get the numerator for the second quadrant. Knowing the pattern for the denominators as presented above allows you to easily remember all of the angle measurements. In the second quadrant, we know the denominators go 3, 4, and 6. Simply subtract 1 digit from the denominator, and you now have the numerator value in the fraction. Just remember to add ???? to the numerator. Here are the radians for the second quadrant angles: A 120 degree angle has a radian of 2????/3. A 135 degree angle has a radian of 3????/4. A 150 degree angle has a radian of 5????/6. A 180 degree angle has a radian of ????. (Remember, this is your negative x-axis, which was discussed above.)

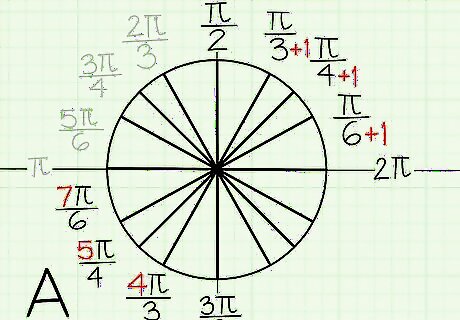
Add 1 to the denominator to get the numerator for the third quadrant. Remember that the denominators in the third quadrant go 6, 4, and 3. The numerator for each radian measurement will be the denominator + 1, multiplied by ????. Here are the radian measurements for the third quadrant: A 210 degree angle has a radian of 7????/6. A 225 degree angle has a radian of 5????/4. A 240 degree angle has a radian of 4????/3. A 270 degree angle has a measurement of 3????/2, since this is your negative y-axis. Luckily, your quadrant trick works for this angle!

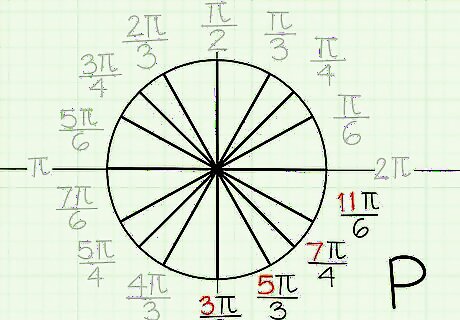
Use the prime numbers to get the numerators for the fourth quadrant. The trick for finding the numerators in the radian measurements for the fourth quadrant comes down to remembering the prime numbers 3, 5, 7, and 11. Here are the angle measurements: The 270 degree angle uses 3 to get a radian of 3????/2. A 300 degree angle has 5 in the denominator, for 5????/3. A 315 degree angle has 7 in the denominator, for 7????/4. A 330 degree angle has 11 in the denominator, for 11????/6. Finally, the circle ends on a 360 degree angle, which has a radian of 2????. (Remember, this is your positive x-axis, as explained above.)

Doing the Left Hand Trick for Sine and Cosine

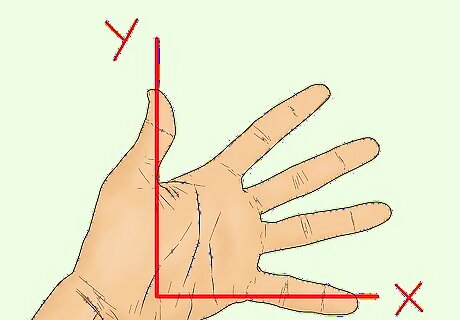
Spread your left palm so your thumb and pinky make a right angle. The first quadrant is the top, right side of the circle. It’s the part of the circle where both the x-coordinate and the y-coordinate are positive. Your thumb and pinky should create a right angle. Your pinky finger will be the x-axis, while your thumb is the y-axis. Cosine is the x-coordinate of an angle, while sine is the y-coordinate of the angle.

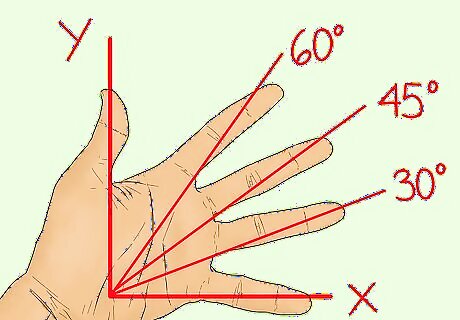
Imagine that each finger represents an angle in the first quadrant. As you move into other quadrants, the angle measurement will change. However, the coordinates for sine and cosine will be the same integer, though they may shift from positive to negative. That means you can use your left hand trick to find the coordinates in any quadrant! Here’s how to label your fingers: Use your pinky to represent a 0 degree angle. The 0 degree angle falls on your x-axis. It’s the starting point of your circle, which is why it’s 0. Your ring finger represents a 30 degree angle. Let your middle finger represent a 45 degree angle. Your index finger represents a 60 degree angle. Make your thumb represent the 90 degree angle.

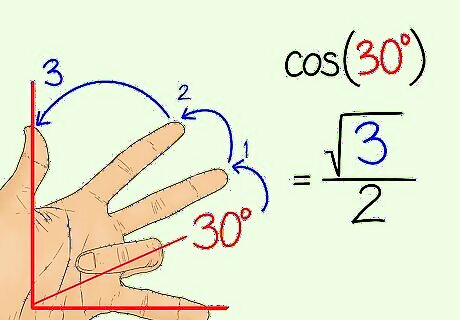
Find the cosine coordinate of an angle by counting the fingers to the left. Put down the finger you’re using to represent the angle you want to find the cosine for. Count the number of fingers to the left of the finger that represents your angle. Then, take the square root of this number and divide it by 2 to find your coordinates. For example, if you were finding the coordinates for a 30 degree angle, you’d put down your ring finger. To the left of that finger, you have your thumb, index finger, and middle finger, which means 3 fingers. This means the cosine coordinate is 3 2 {\displaystyle {\frac {\sqrt {3}}{2}}} {\frac {{\sqrt {3}}}{2}}. This is your final answer since you can't simplify the fraction any further. If you were getting the cosine for a 0 degree angle, you’d put down your pinkie and count 4 fingers to the left. Your equation is 4 2 {\displaystyle {\frac {\sqrt {4}}{2}}} {\frac {{\sqrt {4}}}{2}}. Since the square root of 4 is 2, you’d solve 2/2=1. This is your cosine.

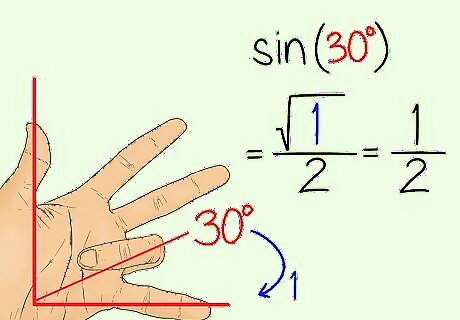
Get the sine coordinate of an angle by counting the fingers to the right. Put your finger down again, then count the number of fingers to the right. Take the square root of this number, then divide it by 2. In the example above, you’d see that for a 30 degree angle you only have one finger to the right, your pinky finger. That means your sine coordinate would be 1 2 {\displaystyle {\frac {\sqrt {1}}{2}}} {\frac {{\sqrt {1}}}{2}}. Since the square root of 1 is 1, you can just write 1/2. For your 0 degree angle, you’d see that there are no fingers to the right of your pinky. This means your sine must be 0.

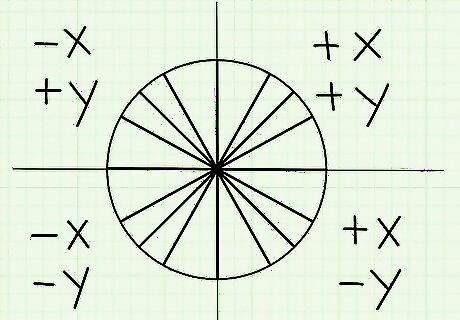
Switch the charge on your coordinates to represent other quadrants. Each quadrant has its own different positive or negative charge. It’s easiest to see this charge when you look at the circle on a grid. The first quadrant is between the positive x-axis and positive y-axis, so both coordinates are positive. The second quadrant is between the positive y-axis and negative x-axis, so it will be negative, positive. Here’s how each coordinate is charged in each quadrant: Quadrant 1 coordinates are (+,+). Quadrant 2 coordinates are (-,+). Quadrant 3 coordinates are (-,-). Quadrant 4 coordinates are (+,-).

Fill in your unit circle using your hand trick. You can use the hand trick to fill in the coordinates for each quadrant, even though the angles are different. Just remember to switch up the positive or negative charges depending on the quadrant you’re doing.

Trying Fun Memorization Tricks

Sing a unit circle song. Putting information to a melody is a great way to help you remember it. You can choose a tune you already like and make up your own song, or you can learn someone else’s unit circle song. Practice singing it to yourself aloud, then you can sing it in your head when you need to remember the unit circle. Here’s a song you might try memorizing: https://www.youtube.com/watch?time_continue=101&v=1CiXAP8XaBg

Play a unit circle game online. You can find online games to play for free. They can help you practice filling in a unit circle while also having fun! Games are a great way to test your knowledge and find out what you need to study more. Plus, you’ll be studying the unit circle without getting bored. You can find unit circle games here: https://www.mathwarehouse.com/unit-circle/unit-circle-game.php https://www.sporcle.com/games/mhershfield/unit-circle-picture-click https://www.purposegames.com/game/unit-circle-quiz

Use flash cards if you prefer to memorize facts. You can make your own flashcards or find pre-made flashcards online. You might study the information by quadrant or by angle measurement. You might find it helpful to create multiple sets of flashcards chunking the information in different ways. You can try pre-made flashcards on Quizlet: https://quizlet.com/17071364/unit-circle-degreesradianssinecosine-flash-cards/ or https://quizlet.com/30187064/sin-cos-and-tan-of-the-unit-circle-radians-flash-cards/