How to Find the Measurement of the Diagonal Inside a Rectangle

Using the Length and the Width

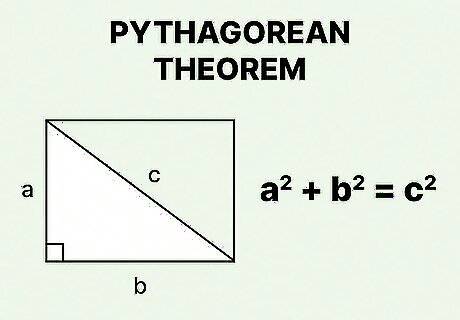
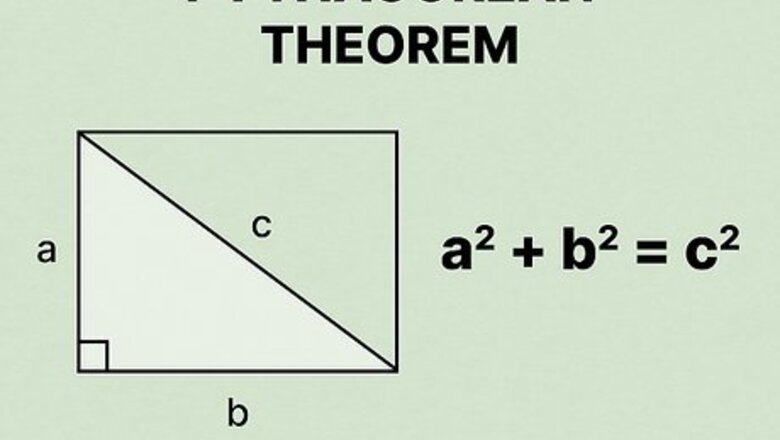
Set up the formula for the Pythagorean Theorem. The formula is a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{{2}}+b^{{2}}=c^{{2}}, where a {\displaystyle a} a and b {\displaystyle b} b equal the side lengths of a right triangle, and c {\displaystyle c} c equals the length of a right triangle’s hypotenuse. You use the Pythagorean Theorem because a diagonal of a rectangle cuts the rectangle into two congruent right triangles. The length and width of the rectangle are the side lengths of the triangle; the diagonal is the hypotenuse of the triangle.

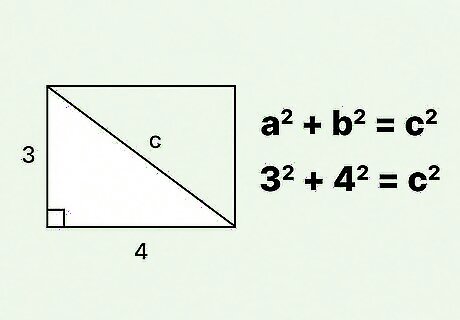
Plug the length and the width into the formula. These should be given, or you should be able to measure them. Make sure you are substituting for a {\displaystyle a} a and b {\displaystyle b} b. For example, if the width of a rectangle is 3 cm, and the length is 4 cm, your formula will look like this: 3 2 + 4 2 = c 2 {\displaystyle 3^{2}+4^{2}=c^{2}} 3^{{2}}+4^{{2}}=c^{{2}}.

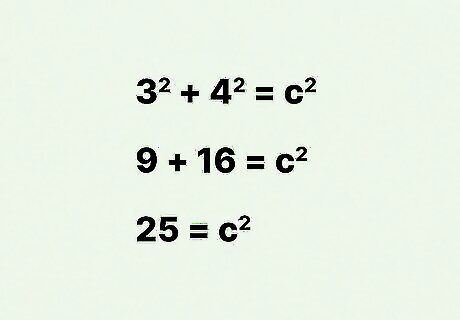
Square the length and width, then add these numbers together. Remember, squaring a number means to multiply the number by itself. For example: 3 2 + 4 2 = c 2 {\displaystyle 3^{2}+4^{2}=c^{2}} 3^{{2}}+4^{{2}}=c^{{2}} 9 + 16 = c 2 {\displaystyle 9+16=c^{2}} 9+16=c^{{2}} 25 = c 2 {\displaystyle 25=c^{2}} 25=c^{{2}}

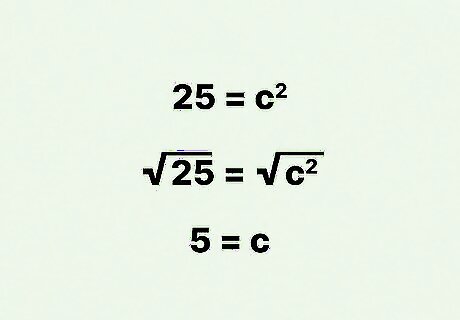
Take the square root of each side of the equation. The easiest way to find a square root is to use a calculator. You can use an online calculator if you do not have a scientific calculator. This will give you the value of c {\displaystyle c} c, which is the hypotenuse of the triangle, and the diagonal of the rectangle. For example: 25 = c 2 {\displaystyle 25=c^{2}} 25=c^{{2}} 25 = c 2 {\displaystyle {\sqrt {25}}={\sqrt {c^{2}}}} {\sqrt {25}}={\sqrt {c^{{2}}}} 5 = c {\displaystyle 5=c} 5=cSo, the diagonal of a rectangle with a width of 3 cm and a length of 4 cm is 5 cm.

Using the Area and Perimeter

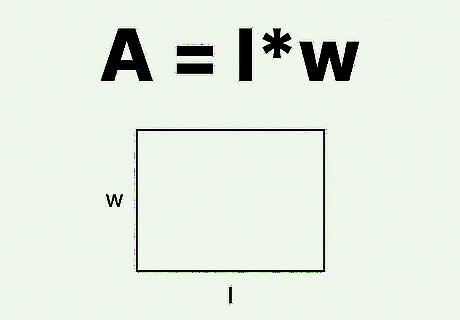
Set up the formula for the area of a rectangle. The formula is A = l w {\displaystyle A=lw} A=lw, where A {\displaystyle A} A equals the area of the rectangle, l {\displaystyle l} l equals the length of the rectangle, and w {\displaystyle w} w equals the width of the rectangle.

Plug the area of the rectangle into the formula. Make sure you substitute for the variable A {\displaystyle A} A. For example, if the area of the rectangle is 35 square centimeters, your formula will look like this: 35 = l w {\displaystyle 35=lw} 35=lw.

Rearrange the formula, finding a value for w {\displaystyle w} w. To do this, divide both sides of the equation by l {\displaystyle l} l. Set this value aside. You will plug it into the perimeter formula later. For example: 35 = l w {\displaystyle 35=lw} 35=lw 35 l = w {\displaystyle {\frac {35}{l}}=w} {\frac {35}{l}}=w.

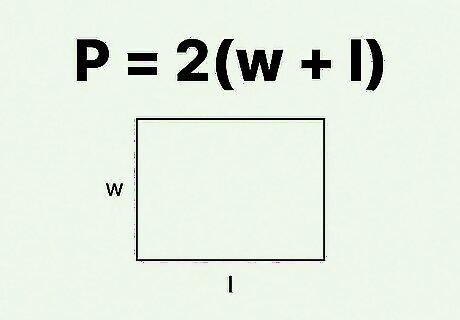
Set up the formula for the perimeter of a rectangle. The formula is P = 2 ( w + l ) {\displaystyle P=2(w+l)} P=2(w+l), where w {\displaystyle w} w equals the width of the rectangle, and l {\displaystyle l} l equals the length of the rectangle.

Plug the value of the perimeter into the formula. Make sure you substitute for the variable P {\displaystyle P} P. For example, if the perimeter of a rectangle is 24 centimeters, your formula will look like this: 24 = 2 ( w + l ) {\displaystyle 24=2(w+l)} 24=2(w+l).

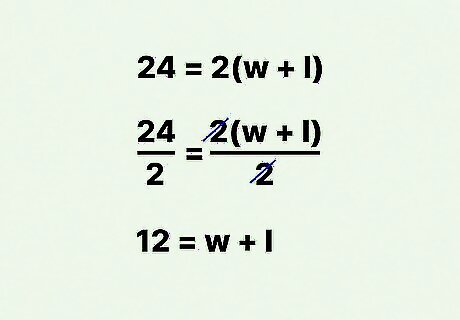
Divide both sides of the equation by 2. This will give you the value of w + l {\displaystyle w+l} w+l. For example: 24 = 2 ( w + l ) {\displaystyle 24=2(w+l)} 24=2(w+l) 24 2 = 2 ( w + l ) 2 {\displaystyle {\frac {24}{2}}={\frac {2(w+l)}{2}}} {\frac {24}{2}}={\frac {2(w+l)}{2}} 12 = w + l {\displaystyle 12=w+l} 12=w+l.

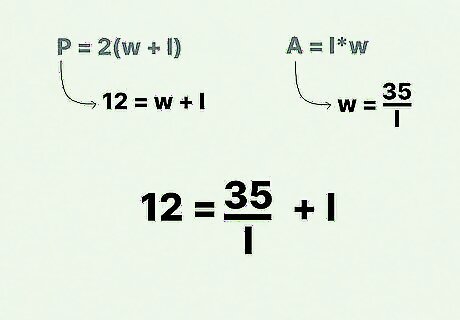
Plug the value of w {\displaystyle w} w into the equation. Use the value you found by rearranging the formula for area. For example, if using the area formula you found that 35 l = w {\displaystyle {\frac {35}{l}}=w} {\frac {35}{l}}=w, replace this value of w {\displaystyle w} w into the perimeter formula: 12 = w + l {\displaystyle 12=w+l} 12=w+l 12 = 35 l + l {\displaystyle 12={\frac {35}{l}}+l} 12={\frac {35}{l}}+l

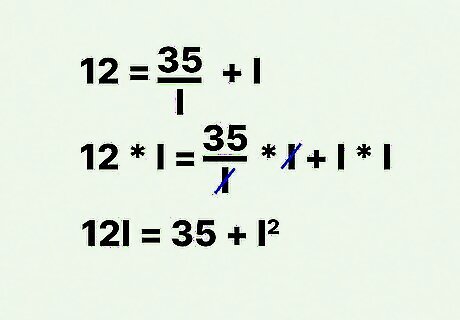
Cancel out the fraction in the equation. To do this, multiply both sides of the equation by l {\displaystyle l} l. For example: 12 = 35 l + l {\displaystyle 12={\frac {35}{l}}+l} 12={\frac {35}{l}}+l 12 × l = ( 35 l × l ) + ( l × l ) {\displaystyle 12\times l=({\frac {35}{l}}\times l)+(l\times l)} 12\times l=({\frac {35}{l}}\times l)+(l\times l) 12 l = 35 + l 2 {\displaystyle 12l=35+l^{2}} 12l=35+l^{{2}}

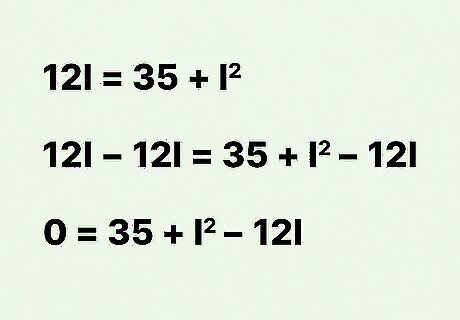
Set the equation to 0. To do this, subtract the first-degree term from both sides of the equation. For example: 12 l = 35 + l 2 {\displaystyle 12l=35+l^{2}} 12l=35+l^{{2}} 12 l − 12 l = 35 + l 2 − 12 l {\displaystyle 12l-12l=35+l^{2}-12l} 12l-12l=35+l^{{2}}-12l 0 = 35 + l 2 − 12 l {\displaystyle 0=35+l^{2}-12l} 0=35+l^{{2}}-12l

Reorder the equation by order of terms. This means the term with the exponent will be first, followed by the term with the variable, followed by the constant. When reordering, make sure you keep the appropriate positive and negative signs. You should note that the equation is now set up as a quadratic equation. For example, 0 = 35 + l 2 − 12 l {\displaystyle 0=35+l^{2}-12l} 0=35+l^{{2}}-12l becomes 0 = l 2 − 12 l + 35 {\displaystyle 0=l^{2}-12l+35} 0=l^{{2}}-12l+35.

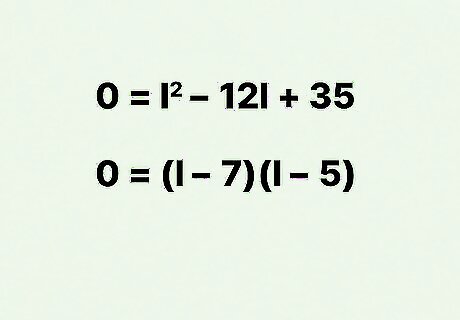
Factor the quadratic equation. For complete instructions on how to do this, read Solve Quadratic Equations. For example, the equation 0 = l 2 − 12 l + 35 {\displaystyle 0=l^{2}-12l+35} 0=l^{{2}}-12l+35 can be factored as 0 = ( l − 7 ) ( l − 5 ) {\displaystyle 0=(l-7)(l-5)} 0=(l-7)(l-5).

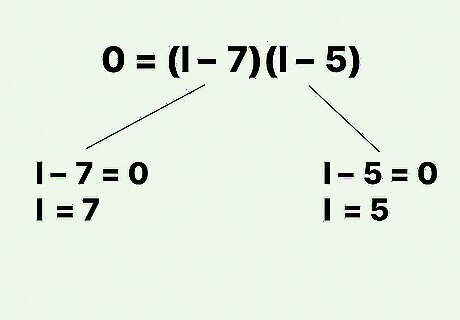
Find the values of l {\displaystyle l} l. To do this, set each term to zero and solve for the variable. You will find two solutions, or roots, to the equation. Since you are working with a rectangle, the two roots will be the width and length of your rectangle. For example: 0 = ( l − 7 ) {\displaystyle 0=(l-7)} 0=(l-7) 7 = l {\displaystyle 7=l} 7=lAND 0 = ( l − 5 ) {\displaystyle 0=(l-5)} 0=(l-5) 5 = l {\displaystyle 5=l} 5=l.So, the length and width of the rectangle are 7 cm and 5 cm.

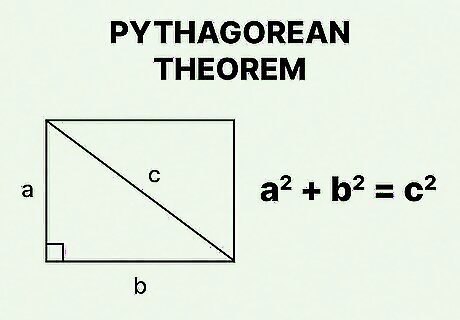
Set up the formula for the Pythagorean Theorem. The formula is a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{{2}}+b^{{2}}=c^{{2}}, where a {\displaystyle a} a and b {\displaystyle b} b equal the side lengths of a right triangle, and c {\displaystyle c} c equals the length of a right triangle’s hypotenuse. You use the Pythagorean Theorem because a diagonal of a rectangle cuts the rectangle into two congruent right triangles. The width and length of the rectangle are the side lengths of the triangle; the diagonal is the hypotenuse of the triangle.

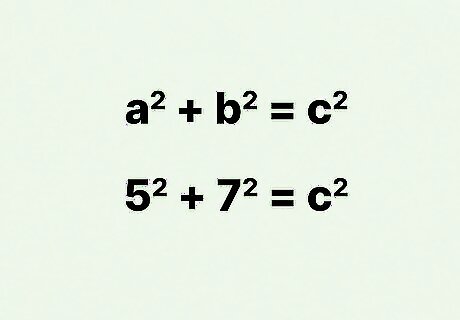
Plug the width and length into the formula. It doesn’t matter which value you use for which variable. For example, if you found the width and length of the rectangle are 5 cm and 7 cm, your formula will look like this: 5 2 + 7 2 = c 2 {\displaystyle 5^{2}+7^{2}=c^{2}} 5^{{2}}+7^{{2}}=c^{{2}}.

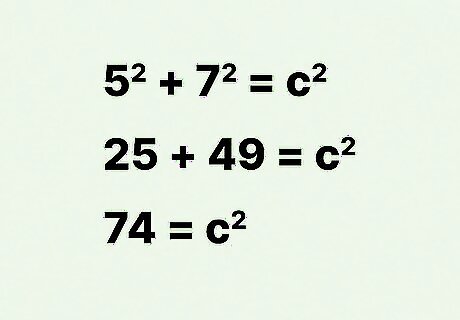
Square the width and length, then add these numbers together. Remember, squaring a number means to multiply the number by itself. For example: 5 2 + 7 2 = c 2 {\displaystyle 5^{2}+7^{2}=c^{2}} 5^{{2}}+7^{{2}}=c^{{2}} 25 + 49 = c 2 {\displaystyle 25+49=c^{2}} 25+49=c^{{2}} 74 = c 2 {\displaystyle 74=c^{2}} 74=c^{{2}}

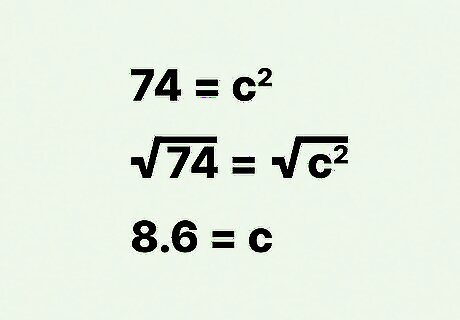
Take the square root of each side of the equation. The easiest way to find a square root is to use a calculator. You can use an online calculator if you do not have a scientific calculator. This will give you the value of c {\displaystyle c} c, which is the hypotenuse of the triangle, and the diagonal of the rectangle. For example: 74 = c 2 {\displaystyle 74=c^{2}} 74=c^{{2}} 74 = c 2 {\displaystyle {\sqrt {74}}={\sqrt {c^{2}}}} {\sqrt {74}}={\sqrt {c^{{2}}}} 8.6024 = c {\displaystyle 8.6024=c} 8.6024=cSo, the diagonal of a rectangle with an area of 35 cm and a perimeter of 24 cm is about 8.6 cm.

Using the Area and Relational Side Lengths

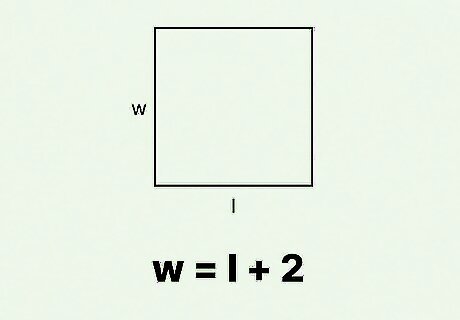
Write a formula explaining the relationship between the side lengths. You can isolate the length ( l {\displaystyle l} l) or the width ( w {\displaystyle w} w). Set this formula aside. You will plug it into the area formula later. For example, if you know the width of a rectangle is 2 cm more than the length, you can write a formula for w {\displaystyle w} w: w = l + 2 {\displaystyle w=l+2} w=l+2.

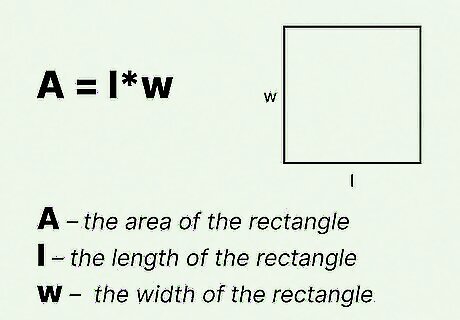
Set up the formula for the area of a rectangle. The formula is A = l w {\displaystyle A=lw} A=lw, where A {\displaystyle A} A equals the area of the rectangle, l {\displaystyle l} l equals the length of the rectangle, and w {\displaystyle w} w equals the width of the rectangle. You can use this method if you know the perimeter of the rectangle, except you would now set up the perimeter formula instead of the area formula. The formula for the perimeter of a rectangle is P = 2 ( w + l ) {\displaystyle P=2(w+l)} P=2(w+l), where w {\displaystyle w} w equals the width of the rectangle, and l {\displaystyle l} l equals the length of the rectangle.

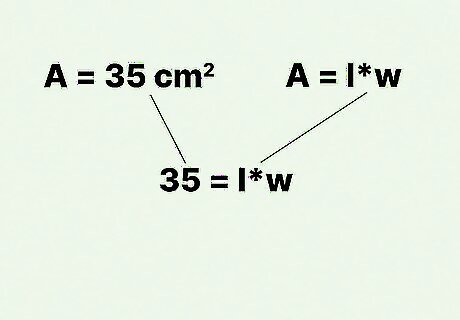
Plug the area of the rectangle into the formula. Make sure you substitute for the variable A {\displaystyle A} A. For example, if the area of the rectangle is 35 square centimeters, your formula will look like this: 35 = l w {\displaystyle 35=lw} 35=lw.

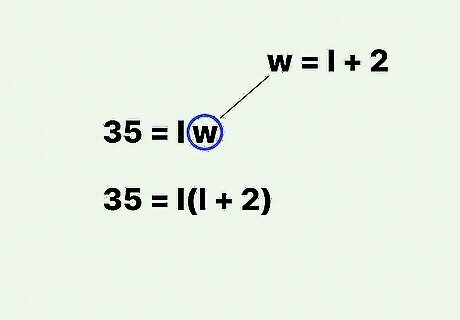
Plug the relational formula for the length (or width) into the formula. Since you are working with a rectangle, it doesn’t matter whether you work with the l {\displaystyle l} l or w {\displaystyle w} w variable. For example, if you found that w = l + 2 {\displaystyle w=l+2} w=l+2, then you would substitute this relationship for w {\displaystyle w} w in the area formula: 35 = l w {\displaystyle 35=lw} 35=lw 35 = l ( l + 2 ) {\displaystyle 35=l(l+2)} 35=l(l+2)

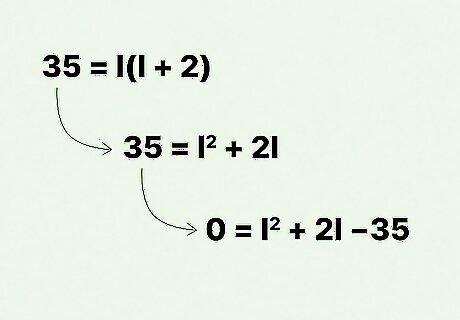
Set up a quadratic equation. To do this, use the distributive property to multiply the terms in parentheses, then set the equation to 0. For example: 35 = l ( l + 2 ) {\displaystyle 35=l(l+2)} 35=l(l+2) 35 = l 2 + 2 l {\displaystyle 35=l^{2}+2l} 35=l^{{2}}+2l 0 = l 2 + 2 l − 35 {\displaystyle 0=l^{2}+2l-35} 0=l^{{2}}+2l-35

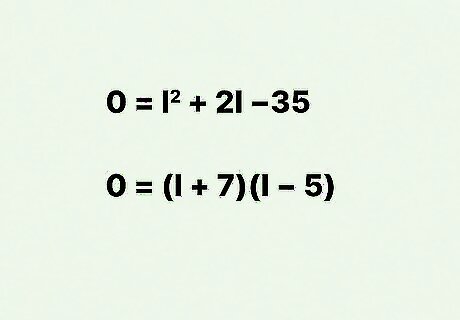
Factor the quadratic equation. For complete instructions on how to do this, read Solve Quadratic Equations. For example, the equation 0 = l 2 + 2 l − 35 {\displaystyle 0=l^{2}+2l-35} 0=l^{{2}}+2l-35 can be factored as 0 = ( l + 7 ) ( l − 5 ) {\displaystyle 0=(l+7)(l-5)} 0=(l+7)(l-5).

Find the values of l {\displaystyle l} l. To do this, set each term to zero and solve for the variable. You will find two solutions, or roots, to the equation. For example: 0 = ( l + 7 ) {\displaystyle 0=(l+7)} 0=(l+7) − 7 = l {\displaystyle -7=l} -7=lAND 0 = ( l − 5 ) {\displaystyle 0=(l-5)} 0=(l-5) 5 = l {\displaystyle 5=l} 5=l.In this case, you have one negative root. Since the length of a rectangle cannot be negative, you know that the length must be 5 cm.

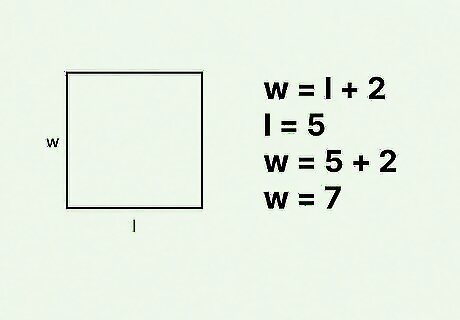
Plug the value of the length (or width) into your relationship formula. This will give you the length of the other side of the rectangle. For example, if you know that the length of the rectangle is 5 cm, and that the relationship between the side lengths is w = l + 2 {\displaystyle w=l+2} w=l+2, you would substitute 5 for the length in the formula: w = l + 2 {\displaystyle w=l+2} w=l+2 w = 5 + 2 {\displaystyle w=5+2} w=5+2 w = 7 {\displaystyle w=7} w=7

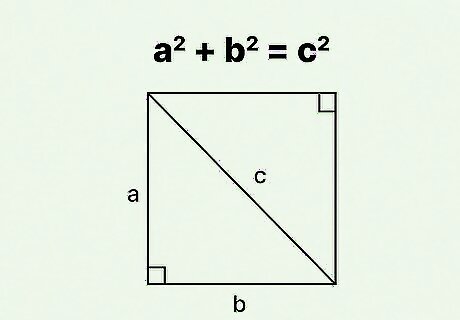
Set up the formula for the Pythagorean Theorem. The formula is a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} a^{{2}}+b^{{2}}=c^{{2}}, where a {\displaystyle a} a and b {\displaystyle b} b equal the side lengths of a right triangle, and c {\displaystyle c} c equals the length of a right triangle’s hypotenuse. You use the Pythagorean Theorem because a diagonal of a rectangle cuts the rectangle into two congruent right triangles. The width and length of the rectangle are the side lengths of the triangle; the diagonal is the hypotenuse of the triangle.

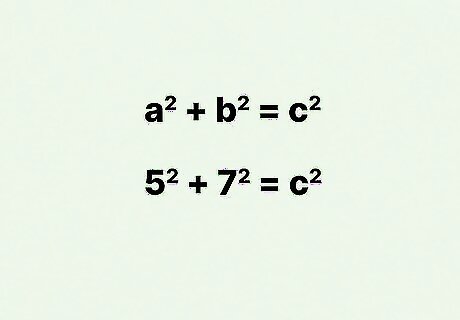
Plug the width and length into the formula. It doesn’t matter which value you use for which variable. For example, if you found the width and length of the rectangle are 5 cm and 7 cm, your formula will look like this: 5 2 + 7 2 = c 2 {\displaystyle 5^{2}+7^{2}=c^{2}} 5^{{2}}+7^{{2}}=c^{{2}}.

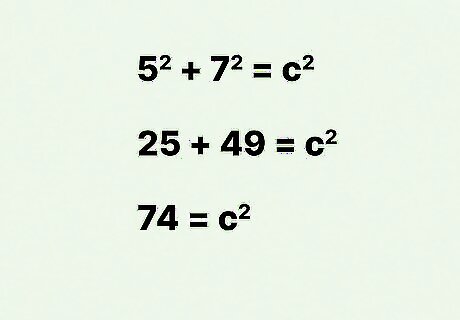
Square the width and length, then add these numbers together. Remember, squaring a number means to multiply the number by itself. For example: 5 2 + 7 2 = c 2 {\displaystyle 5^{2}+7^{2}=c^{2}} 5^{{2}}+7^{{2}}=c^{{2}} 25 + 49 = c 2 {\displaystyle 25+49=c^{2}} 25+49=c^{{2}} 74 = c 2 {\displaystyle 74=c^{2}} 74=c^{{2}}

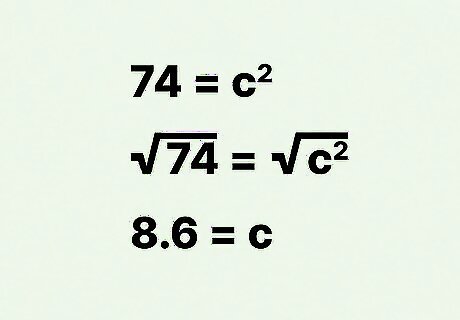
Take the square root of each side of the equation. The easiest way to find a square root is to use a calculator. You can use an online calculator if you do not have a scientific calculator. This will give you the value of c {\displaystyle c} c, which is the hypotenuse of the triangle, and the diagonal of the rectangle. For example: 74 = c 2 {\displaystyle 74=c^{2}} 74=c^{{2}} 74 = c 2 {\displaystyle {\sqrt {74}}={\sqrt {c^{2}}}} {\sqrt {74}}={\sqrt {c^{{2}}}} 8.6024 = c {\displaystyle 8.6024=c} 8.6024=cSo, the diagonal of a rectangle with a width that is 2 cm more than the length, and an area of 35 cm, is about 8.6 cm.