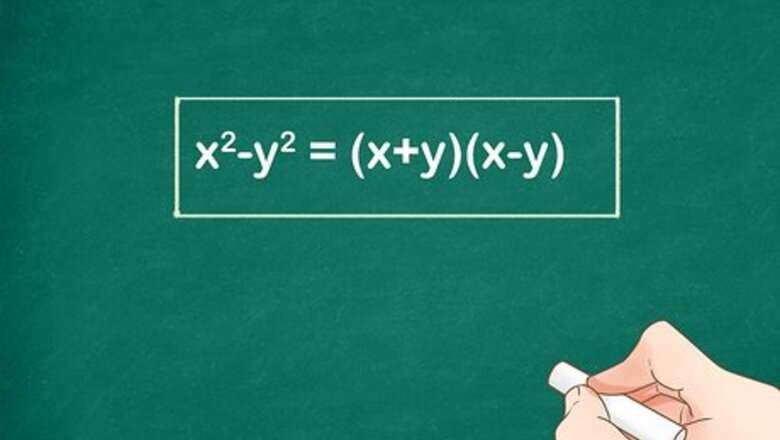
views
Using Difference of Squares for Factors with an Even Difference
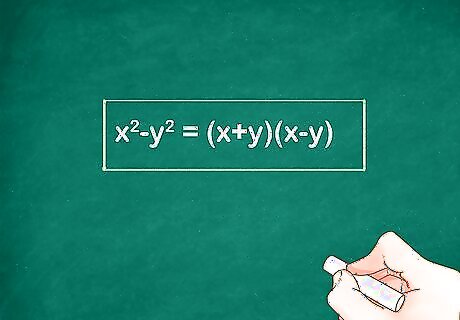
Set up a difference of squares formula. The difference of squares formula states that ( x − y ) ( x + y ) = x 2 − y 2 {\displaystyle (x-y)(x+y)=x^{2}-y^{2}} (x-y)(x+y)=x^{{2}}-y^{{2}}. In the formula, x {\displaystyle x} x = the number equidistant from the two factors, and y {\displaystyle y} y = half the difference between the two factors.

Subtract one factor from the other. Determine whether their difference is even or odd. If their difference is even, that means they are equidistant from another number, and you can use the difference of squares method. A factor is a number being multiplied by another number. If the difference between factors is odd, then you can still use the difference of squares method to solve, but you will have to manipulate the problem, as described in Method 2. For example, if you were multiplying 28 × 32 {\displaystyle 28\times 32} 28\times 32, you could use the difference of squares method, because 28 − 32 = − 4 {\displaystyle 28-32=-4} 28-32=-4, and -4 is an even number. It doesn't matter if the difference is positive or negative. A difference of -4 is the same as a difference of 4. Both +/-4 are even.

Divide the difference between the two factors by 2. Plug in this number for y {\displaystyle y} y in the difference of squares formula. For example, you already found that the difference between 28 and 32 is 4. 4 ÷ 2 = 2 {\displaystyle 4\div 2=2} 4\div 2=2. So half the difference between the two factors is 2. Plugging in this number for y {\displaystyle y} y, your formula becomes ( x − 2 ) ( x + 2 ) = x 2 − 2 2 {\displaystyle (x-2)(x+2)=x^{2}-2^{2}} (x-2)(x+2)=x^{{2}}-2^{{2}}.

Find the number equidistant from the two factors. To do this, take the larger factor and subtract it by half the difference between the two factors ( y {\displaystyle y} y in your difference of squares formula). For example, if the larger factor is 32, and half the difference between factors ( y {\displaystyle y} y) is 2, then you would find the equidistant number by subtracting 2 from 32. 32 − 2 = 30 {\displaystyle 32-2=30} 32-2=30, so the equidistant number is 30. You could also find the equidistant number by taking the smaller factor and adding half the difference.

Plug the equidistant number into the difference of squares formula. To do this, replace all the x {\displaystyle x} xs in the formula with the equidistant number. For example, if your equidistant number is 30, your difference of squares formula will look like this: ( 30 − 2 ) ( 30 + 2 ) = 30 2 − 2 2 {\displaystyle (30-2)(30+2)=30^{2}-2^{2}} (30-2)(30+2)=30^{{2}}-2^{{2}}. Note that ( 30 − 2 ) ( 30 + 2 ) {\displaystyle (30-2)(30+2)} (30-2)(30+2) is the same as ( 28 ) ( 32 ) {\displaystyle (28)(32)} (28)(32), which was your original problem.

Square the two numbers. Plug these squares into the equation. Remember, to square something means to multiply it by itself. For example: 30 2 − 2 2 {\displaystyle 30^{2}-2^{2}} 30^{{2}}-2^{{2}}= 900 − 4 {\displaystyle 900-4} 900-4

Complete the subtraction. The result will equal the answer to your original multiplication problem. For example, 900 − 4 = 896 {\displaystyle 900-4=896} 900-4=896, so 28 × 32 = 896 {\displaystyle 28\times 32=896} 28\times 32=896.

Check your work. You can verify your answer by using a calculator, or by solving using the standard multiplication algorithm.
Using Difference of Squares for Factors With an Odd Difference
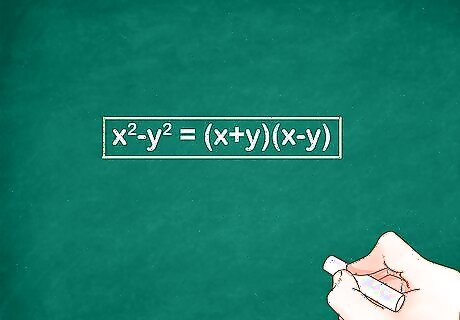
Set up a difference of squares formula. The difference of squares formula states that ( x − y ) ( x + y ) = x 2 − y 2 {\displaystyle (x-y)(x+y)=x^{2}-y^{2}} (x-y)(x+y)=x^{{2}}-y^{{2}}. In the formula, x {\displaystyle x} x = the number equidistant from the two factors, and y {\displaystyle y} y = half the difference between the two factors.

Find the difference between the two factors being multiplied. If the factors are NOT equidistant from another number (that is, the difference is odd), you must follow these instructions to manipulate the difference of squares method. A factor is a number being multiplied by another number. For example, if you were multiplying 35 × 46 {\displaystyle 35\times 46} 35\times 46, you would have to manipulate the difference of squares method, because 35 − 46 = − 11 {\displaystyle 35-46=-11} 35-46=-11, and -11 is an odd number. If the difference between factors is even, use the shortcut described in Method 1.

Subtract 1 from either factor. Subtracting 1 will give you two factors that are equidistant from another number, or two numbers whose difference is even. You will use this manipulated factor to follow the difference of squares method. Do NOT subtract 1 from both factors. Only subtract 1 from one factor. It doesn't matter which one. For example, for 35 × 46 {\displaystyle 35\times 46} 35\times 46 you could subtract 46 − 1 = 45 {\displaystyle 46-1=45} 46-1=45, so your multiplication problem becomes 35 × 45 {\displaystyle 35\times 45} 35\times 45.

Subtract one factor from the other. Make sure you are using the manipulated factor. The difference should now be even. For example, if your new problem, with the manipulated factor, is 35 × 45 {\displaystyle 35\times 45} 35\times 45, the difference between factors is 10, since 35 − 45 = − 10 {\displaystyle 35-45=-10} 35-45=-10. It doesn't matter if the difference is positive or negative. A difference of -10 is the same as a difference of 10. Both +/-10 are even.

Divide the difference between the two factors by 2. Plug in this number for y {\displaystyle y} y in the difference of squares formula. Again, make sure you are using the manipulated factor. For example, you already found that the difference between 35 and 45 is 10. 10 ÷ 2 = 5 {\displaystyle 10\div 2=5} 10\div 2=5. So half the difference between the two factors is 5. Plugging in this number for y {\displaystyle y} y, your formula becomes ( x − 5 ) ( x + 5 ) = x 2 − 5 2 {\displaystyle (x-5)(x+5)=x^{2}-5^{2}} (x-5)(x+5)=x^{{2}}-5^{{2}}

Find the number equidistant from the two factors. To do this, take the larger factor, and subtract it by half the difference between the two factors ( y {\displaystyle y} y in your difference of squares formula). For example, if the larger factor is 45, and half the difference between factors ( y {\displaystyle y} y) is 5, then you would find the equidistant number by subtracting 5 from 45. 45 − 5 = 40 {\displaystyle 45-5=40} 45-5=40, so the equidistant number is 40. You could also find the equidistant number by taking the smaller factor and adding half the difference.

Plug the equidistant number into the difference of squares formula. To do this, replace all the x {\displaystyle x} xs in the formula with the equidistant number. For example, if your equidistant number is 40, your difference of squares formula will look like this: ( 40 − 5 ) ( 40 + 5 ) = 40 2 − 5 2 {\displaystyle (40-5)(40+5)=40^{2}-5^{2}} (40-5)(40+5)=40^{{2}}-5^{{2}}. Note that ( 40 − 5 ) ( 40 + 5 ) {\displaystyle (40-5)(40+5)} (40-5)(40+5) is the same as ( 35 ) ( 45 ) {\displaystyle (35)(45)} (35)(45), the multiplication problem created after manipulating one of the factors.

Square the two numbers. Plug these squares into the equation. Remember, to square something means to multiply it by itself. For example: 40 2 − 5 2 {\displaystyle 40^{2}-5^{2}} 40^{{2}}-5^{{2}}= 1600 − 25 {\displaystyle 1600-25} 1600-25

Complete the subtraction. The result will equal the answer to the multiplication problem with the manipulated factor. For example, 1600 − 25 = 1575 {\displaystyle 1600-25=1575} 1600-25=1575, so 35 × 45 = 1575 {\displaystyle 35\times 45=1575} 35\times 45=1575.
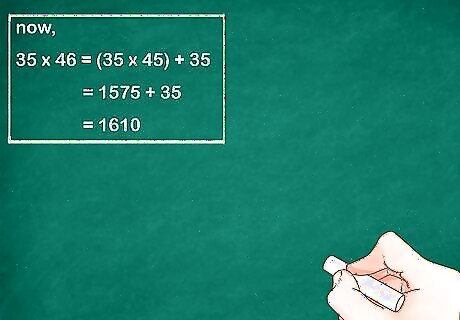
Add the missing value to the answer. Remember, you had to change the initial problem to make the difference of squares method work. To find the answer to the original problem, you must add back in the value you subtracted from the original multiplication problem. You are NOT adding 1 back into the problem. When you subtracted 1, you were really subtracting 1 group, since you are working with multiplication. For example, if the original problem was 35 × 46 {\displaystyle 35\times 46} 35\times 46, that means you were trying to find the value of 46 thirty-fives. When you subtracted 1, you subtracted 1 group of thirty-fives, or 35. Now you need to add that group back in. Since 1575 + 35 = 1610 {\displaystyle 1575+35=1610} 1575+35=1610, you now know that 35 × 46 = 1610 {\displaystyle 35\times 46=1610} 35\times 46=1610.

Check your work. You can verify your answer by using a calculator, or by solving using the standard multiplication algorithm.
















Comments
0 comment