How to Calculate Negative Exponents

Evaluating Negative Exponents

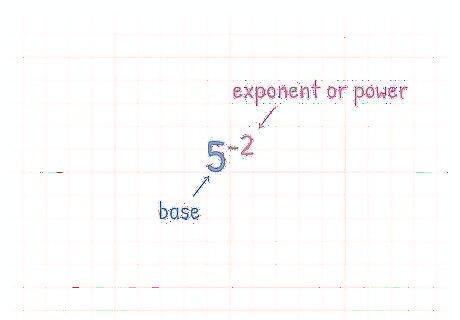
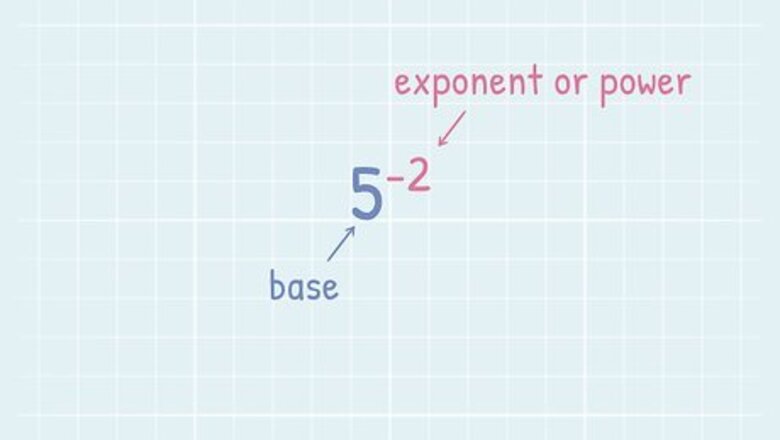
Get to know the basics of negative exponent expression. A negative exponent is usually written as a base number multiplied to the power of a negative number such as 3 − 3 , 5 − 2 , {\displaystyle 3^{-3},5^{-2},} {\displaystyle 3^{-3},5^{-2},} or 7 − 4 {\displaystyle 7^{-4}} {\displaystyle 7^{-4}}. The larger number is known as a base number while the small number is the exponent, in this case the negative exponent. Exponents tell you how many times to multiply a number by itself. Both positive and negative exponents are also referred to as ‘powers’ or numbers that the base number is ‘raised to the power of’. To solve an equation with a negative exponent, you must first make it positive.

Convert negative exponents into fractions to simplify them. A negative exponent tells you that the base number is on the incorrect side of a fraction line. To simplify an expression with a negative exponent, you just flip the base number and exponent to the bottom of a fraction with a 1 {\displaystyle 1} 1 on top. Writing negative exponents as fractions will make it easier for you to understand how to work with them in an equation. To convert a negative exponent, create a fraction with the number 1 as the numerator (top number) and the base number as the denominator (bottom number). Raise the base number to the power of the same exponent, but make it positive. 3 − 3 , 5 − 2 , {\displaystyle 3^{-3},5^{-2},} {\displaystyle 3^{-3},5^{-2},} and 7 − 4 {\displaystyle 7^{-4}} {\displaystyle 7^{-4}} are now 1 ( 3 3 ) , 1 ( 5 2 ) , {\displaystyle {\frac {1}{(3^{3})}},{\frac {1}{(5^{2})}},} {\displaystyle {\frac {1}{(3^{3})}},{\frac {1}{(5^{2})}},} and 1 ( 7 4 ) {\displaystyle {\frac {1}{(7^{4})}}} {\displaystyle {\frac {1}{(7^{4})}}}. This process is known as the negative exponent rule.

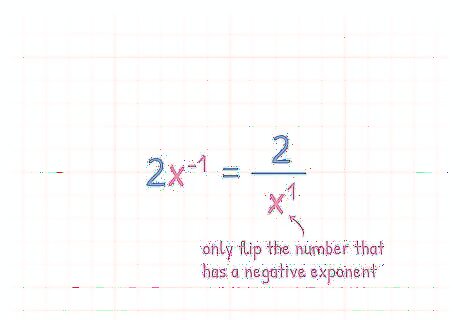
Simplify negative exponent expressions with unknown numbers. Once you understand the negative exponent rule, you can start to simplify more difficult exponent expressions. Things can get tricky at this stage since you will be working with unknown values such as ‘x’ or ‘y’, but luckily the rules to simplify such an equation never change. 2 x − 1 {\displaystyle 2x^{-1}} {\displaystyle 2x^{-1}} can be written as 2 x − 1 1 {\displaystyle {\frac {2x^{-1}}{1}}} {\displaystyle {\frac {2x^{-1}}{1}}} which can then be simplified to 2 ( 1 x 1 ) {\displaystyle {\frac {2}{({1x}^{1})}}} {\displaystyle {\frac {2}{({1x}^{1})}}} 2 1 x 1 {\displaystyle {\frac {2}{1x^{1}}}} {\displaystyle {\frac {2}{1x^{1}}}} can then be simplified to 2 x {\displaystyle {\frac {2}{x}}} {\displaystyle {\frac {2}{x}}} In this case, only ‘x’ became the denominator because it had the exponent.

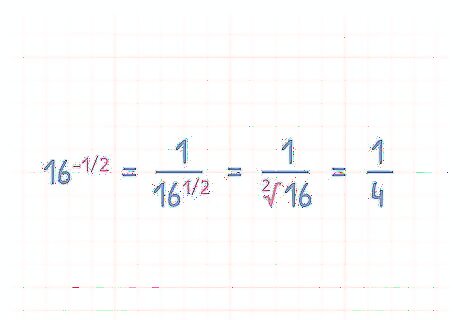
Understand how to solve for negative exponents in fraction form. Sometimes the exponent itself is a fraction. Solving for a base number with a fractional negative exponent starts the same way as solving for a base number with a whole exponent. To simplify a fractional negative exponent, you must first convert to a fraction. If your starting base number is 16 − 1 / 2 {\displaystyle 16^{-1/2}} {\displaystyle 16^{-1/2}}, start by converting it to a fraction where the exponent becomes positive when the base number is switched to the denominator. 16 − 1 / 2 {\displaystyle 16^{-1/2}} {\displaystyle 16^{-1/2}} will become 1 16 1 / 2 {\displaystyle {\frac {1}{16^{1/2}}}} {\displaystyle {\frac {1}{16^{1/2}}}} 1 16 1 / 2 {\displaystyle {\frac {1}{16^{1/2}}}} {\displaystyle {\frac {1}{16^{1/2}}}} is equal to 1 16 2 {\displaystyle {\frac {1}{\sqrt[{2}]{16}}}} {\displaystyle {\frac {1}{\sqrt[{2}]{16}}}} 1 16 2 {\displaystyle {\frac {1}{\sqrt[{2}]{16}}}} {\displaystyle {\frac {1}{\sqrt[{2}]{16}}}} is equal to 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}}.

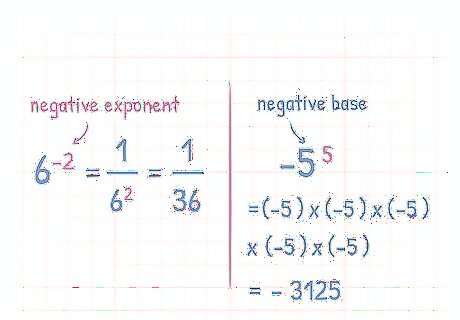
Know the difference between negative bases and negative exponents. Negative bases have different rules than negative exponents when they are used in an equation. They do not need to be converted into fractions if the exponent is positive. Negative negative exponents must be converted into fractions to become positive. When an exponent is negative and a base number is positive, the expression must be converted into a fraction to make the exponent positive For example, 6 − 2 = 1 6 2 {\displaystyle 6^{-2}={\frac {1}{6^{2}}}} {\displaystyle 6^{-2}={\frac {1}{6^{2}}}} When an exponent is positive and a base number is negative, the base number will be multiplied by itself however many times the exponent shows us it should be. For example, − 5 5 = − 5 ∗ − 5 ∗ − 5 ∗ − 5 ∗ − 5 = − 3125. {\displaystyle -5^{5}=-5*-5*-5*-5*-5=-3125.} {\displaystyle -5^{5}=-5*-5*-5*-5*-5=-3125.}

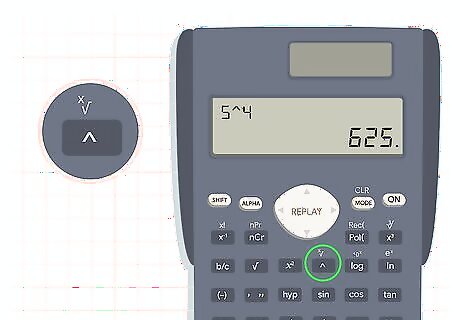
Use a calculator to complete exponent equations quickly. Calculators have specific functions for calculating exponents. Use the E, "^", or "e^x" button to raise any number to any power. Calculators make it easy to check your work and easily convert negative exponents. Remember to put negative exponent values in parentheses: 4 E ( − 6 ) {\displaystyle 4E(-6)} {\displaystyle 4E(-6)} Solving exponential equations on a calculator will allow you to find answers more quickly without converting them into fractions.

Completing Equations with Negative Exponents

Add exponents together if the multiplied base numbers are the same. If two identical base numbers are multiplied, you can add the negative exponents together. The base number will stay the same while the exponent will become a larger negative number. 4 − 1 / 4 ∗ 4 − 1 / 4 {\displaystyle 4^{-1/4}*4^{-1/4}} {\displaystyle 4^{-1/4}*4^{-1/4}} can be simplified to 4 − 1 / 2 {\displaystyle 4^{-1/2}} {\displaystyle 4^{-1/2}} You can further simplify 4 − 1 / 2 {\displaystyle 4^{-1/2}} {\displaystyle 4^{-1/2}} into 1 4 − 1 / 2 {\displaystyle {\frac {1}{4^{-1/2}}}} {\displaystyle {\frac {1}{4^{-1/2}}}} 1 4 − 1 / 2 {\displaystyle {\frac {1}{4^{-1/2}}}} {\displaystyle {\frac {1}{4^{-1/2}}}} becomes 1 4 2 {\displaystyle {\frac {1}{\sqrt[{2}]{4}}}} {\displaystyle {\frac {1}{\sqrt[{2}]{4}}}} which is equal to 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}

Subtract negative exponents if the divided base numbers are the same. Exponents with the same base number can be subtracted from one another. When you divide two base numbers with the same value and different exponents, you simply subtract the exponent values and keep the base number as it is. Because the exponent is negative, the subtraction will cancel out the second negative and make the exponent positive. The exponents in 2 − 7 2 − 2 {\displaystyle {\frac {2^{-7}}{2^{-2}}}} {\displaystyle {\frac {2^{-7}}{2^{-2}}}} will subtract as ( − 7 ) − ( − 2 ) {\displaystyle (-7)-(-2)} {\displaystyle (-7)-(-2)} or ( − 7 ) + 2 {\displaystyle (-7)+2} {\displaystyle (-7)+2} The equation will simplify to 2 − 5 {\displaystyle 2^{-5}} {\displaystyle 2^{-5}} or 1 2 5 {\displaystyle {\frac {1}{2^{5}}}} {\displaystyle {\frac {1}{2^{5}}}}

Keep exponents the same when the base number is different. If two different base numbers with the same exponents are multiplied or divided, do not change the exponent value. When you multiply or divide numbers with different bases and the same negative exponents, the exponent number will not change. Multiply or divide the bases and keep the exponent the same. 7 − 6 ∗ 8 − 6 {\displaystyle 7^{-6}*8^{-6}} {\displaystyle 7^{-6}*8^{-6}} will become 56 − 6 {\displaystyle 56^{-6}} {\displaystyle 56^{-6}} 5 − 1 / 6 ∗ 20 − 1 / 6 {\displaystyle 5^{-1/6}*20^{-1/6}} {\displaystyle 5^{-1/6}*20^{-1/6}} will become 100 − 1 / 6 {\displaystyle 100^{-1/6}} {\displaystyle 100^{-1/6}}

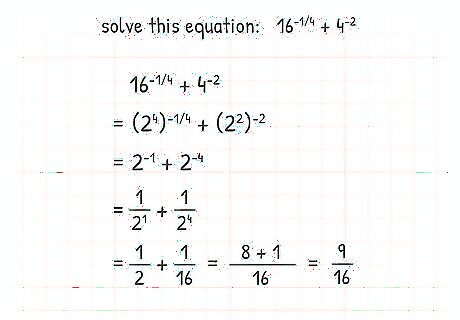
Practice different equations to become a master of negative exponents. Once you understand the basics of working with negative exponents, it is a good idea to challenge yourself with different equations. The rules for negative exponents will never change. Once you learn the basic rules for negative exponents, your math homework will be a breeze. 16 − 1 / 4 + 4 − 2 = 1 16 4 + 1 ( 4 2 ) {\displaystyle 16^{-1/4}+4^{-2}={\frac {1}{\sqrt[{4}]{16}}}+{\frac {1}{(4^{2})}}} {\displaystyle 16^{-1/4}+4^{-2}={\frac {1}{\sqrt[{4}]{16}}}+{\frac {1}{(4^{2})}}} 1 16 4 + 1 ( 4 2 ) = 1 2 + 1 16 {\displaystyle {\frac {1}{\sqrt[{4}]{16}}}+{\frac {1}{(4^{2})}}={\frac {1}{2}}+{\frac {1}{16}}} {\displaystyle {\frac {1}{\sqrt[{4}]{16}}}+{\frac {1}{(4^{2})}}={\frac {1}{2}}+{\frac {1}{16}}} 1 2 + 1 16 = 8 16 + 1 16 {\displaystyle {\frac {1}{2}}+{\frac {1}{16}}={\frac {8}{16}}+{\frac {1}{16}}} {\displaystyle {\frac {1}{2}}+{\frac {1}{16}}={\frac {8}{16}}+{\frac {1}{16}}} 8 16 + 1 16 = 9 16 {\displaystyle {\frac {8}{16}}+{\frac {1}{16}}={\frac {9}{16}}} {\displaystyle {\frac {8}{16}}+{\frac {1}{16}}={\frac {9}{16}}}