How to Calculate Compound Interest Payments

Understanding Compound Interest

Understand the meaning of interest. Interest can be calculated for loans or for investments. For a loan, interest is the amount paid to the creditor for granting the loan to you. For an investment, interest is income that the investment earns. Interest for a loan is usually expressed as an annual percentage rate, which is the annual rate that is charged for borrowing the money. Interest on an investment is usually expressed as a percentage. The two main types of interest that can be applied to loans are simple and compound interest. Simple interest is calculated by multiplying the interest by the principal by the number of periods. Compound interest, however, is the most commonly used method of applying interest to a loan or investment.

Define compound interest. Compound interest is interest calculated on the original principal plus interest calculated on the accumulated interest from previous accounting periods. The rate at which the interest accrues, or accumulates over time, depends on how often the interest is compounded. Interest can be compounded annually, monthly or quarterly. Compound interest is not beneficial for those in debt. If a person carries a credit card balance on a high-interest credit card for which the interest is compounded monthly, the interest payments alone could be hundreds of dollars per month. Compound interest is advantageous to investors, because the interest that is earned each accounting period gets added back to the principal and earns more money for the investor.

Learn the formula for compound interest. The annual compound interest formula is P ( 1 + i ) n − P {\displaystyle P(1+i)^{n}-P} P(1+i)^{n}-P. In this formula, P = Principal, i = annual interest rate in percentage terms, and n = number of compounding periods. If the interest is compounded more than once per year, such as monthly (12 times per year) or quarterly (four times per year), the formula must be adjusted, The formula for compound interest that is compounded multiple times per year is [ P ( 1 + i / n ) n ∗ t ] − P {\displaystyle [P(1+i/n)^{n*t}]-P} [P(1+i/n)^{{n*t}}]-P. In this formula, P = Principal, i = interest rate, n = number of compounding periods, and t = the number of years for which the money is invested or borrowed.

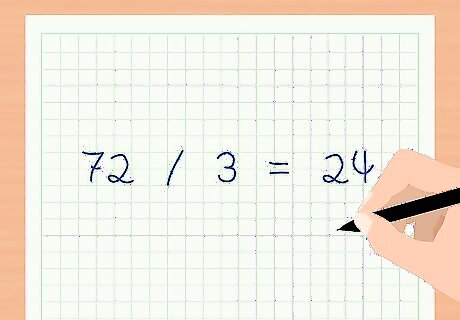
Understand the Rule of 72. You can use the rule of 72 to figure out how long it will take to double your money on an investment that is earning compound interest. Divide 72 by the annual interest rate your investment is earning. The answer will tell you how many years it will take for your investment to double in value. For example, if your investment is earning a 3 percent interest rate, calculate how long it will take to double your money using the equation 72 / 3 = 24 {\displaystyle 72/3=24} 72/3=24. In 24 years, your investment will have doubled in value. Interest rates on investments do fluctuate, so the rule of 72 should be used as a tool for estimating the future value of your investments.

Using an Online Calculator to Find Compound Interest

Access the online calculator. Go to https://www.investor.gov/tools/calculators/compound-interest-calculator to access the compound interest calculator. This calculator is provided by the Securities and Exchange Commission's website Investor.gov.

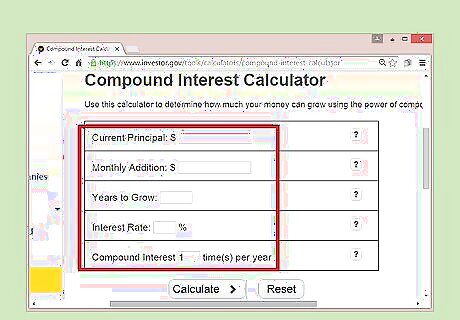
Understand your variables. On the page, you will be asked to input several variables. These should be entered as follows: Current principal: this is how much you initially invested or the original amount on your loan. An investment should be entered as a positive number while a loan amount should be entered as a negative number (using a "-" sign). Monthly addition. If you regularly add an amount to your investment or pay down your loan at regular intervals, input the amount paid each time as a positive number. Years to grow. This is the time period you are looking at in years. This can also be the life of your loan. Interest rate. Input the interest rate your investment earns or the amount you pay on your loans. This is the annual rate. Compound interest __ times per year. Input 1 for annual compounding, 2 for semiannual, 4 for quarterly, or 12 for monthly, depending on how your investment or loan compounds. This information should be available on an investment prospectus or loan document.

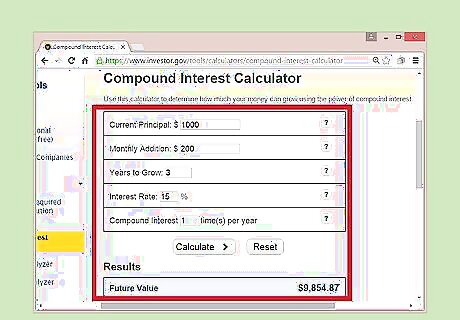
Calculate compound interest earned on investments. To calculate interest earned on investments, start by inputting the amount that you initially invested. Be sure to include any payments you make on a monthly basis in the "monthly addition" box. Then, enter the number of years you want to track investment growth over. Next, input your interest rate. This can be an expected interest rate if you are unsure. Finally, input how many times your investment interest is compounded each year. You can play around with these variables and use them to compare different investment opportunities or different interest rates and compounding frequencies.

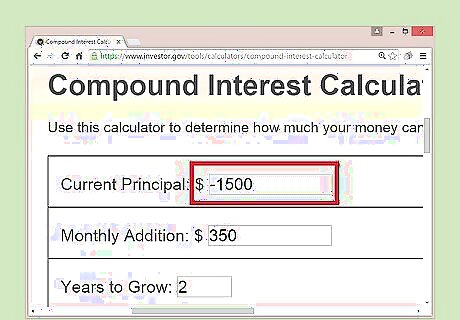
Calculate compound interest charged on loans. Because this is technically an investment calculator, finding interest on loans is a bit different. First, you'll have to enter the principal on the loan as a negative number. This lets the calculator know that you owe the money instead of owning it. For monthly addition, input how much you are able to pay down the loan each month. This can be a minimum payment, a budgeted amount, or any other amount that you can pay each month. Input the rest of the variables as normal. If your result is negative, you will still owe money at the end of the timeframe. However, a positive number reflect that you can pay off the loan in this way by the end of the period.

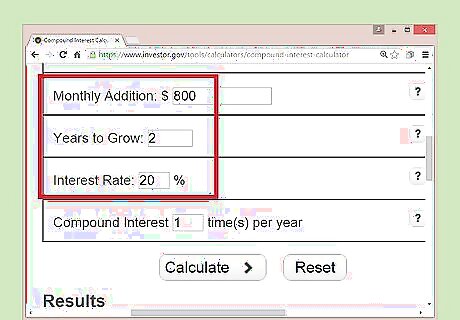
Finding monthly payments. You can also use this calculator and some guesswork to determine the right monthly payments for you. Say, for example, you owe $20,000 on a credit card that charges 20% interest compounded monthly. You want to pay off the card in two years, but don't know how much to pay each month to do. Start by guessing a proper monthly payment. For example, $800. By inputting this data, you'll see that you'll still owe $6,336.39 at the end of the two years if you pay $800 each month. Increase your guess. For example, $1000. This one is much closer and leaves you with only about $523 to pay at the end of the two years. Continue this process until you arrive at an approximate monthly payment that suits your needs.

Calculating Compound Interest Payments on Investments

Calculate annual compound interest on an investment. Suppose you deposited $1,500 into a bank account. The account earns 4.3 percent interest annually. The interest is compounded annually, or one time per year. Suppose you want to find out how much compound interest you will have earned after six years.

Apply the formula. The formula for annual compound interest is [ P ( 1 + i ) n ] − P {\displaystyle [P(1+i)^{n}]-P} [P(1+i)^{n}]-P, where P = Principal, i = interest rate and n = number of compounding periods. For this example, P = $1,500, i = .043 and n = 6 (because if the interest is compounded annually, then in six years there will be six compounding periods). Calculate the interest paid in six years with the equation [ $ 1 , 500 ( 1 + .043 ) 6 ] − $ 1 , 500 {\displaystyle [\$1,500(1+.043)^{6}]-\$1,500} [\$1,500(1+.043)^{6}]-\$1,500 $ 1 , 500 ∗ 1.287 − $ 1 , 500 {\displaystyle \$1,500*1.287-\$1,500} \$1,500*1.287-\$1,500 $ 1 , 931 − $ 1 , 500 = $ 431 {\displaystyle \$1,931-\$1,500=\$431} \$1,931-\$1,500=\$431 The amount of compound interest paid in six years is $431.

Calculate quarterly compound interest. Suppose you deposited $1,500 into an account that paid 4.3 percent interest that was compounded quarterly, or four times per year. To calculate how much interest you would be paid in six years, you would use the formula [ P ( 1 + i / n ) n ∗ t ] − P {\displaystyle [P(1+i/n)^{n*t}]-P} [P(1+i/n)^{{n*t}}]-P, where P = Principal, i = interest rate, n = number of compounding periods per year, and t = the number of years for which the money is invested. In this example, P = $1,500, i = .043, n = 4 and t = 6. You would calculate [ $ 1500 ( 1 + .043 / 4 ) 4 ∗ 6 ] − $ 1500 {\displaystyle [\$1500(1+.043/4)^{4*6}]-\$1500} [\$1500(1+.043/4)^{{4*6}}]-\$1500 ( $ 1 , 500 ∗ 1.29 ) − $ 1 , 500 {\displaystyle (\$1,500*1.29)-\$1,500} (\$1,500*1.29)-\$1,500 $ 1 , 938 − $ 1500 = $ 438 {\displaystyle \$1,938-\$1500=\$438} \$1,938-\$1500=\$438. The amount of compound interest paid in six years is $438.

Calculating Compound Interest Payments on Loans

Understand how compound interest works in loans. Compound interest is calculated on loans using the same formulas. However, instead of earning you a lot of money, compound interest on loans can cost you a lot of money. High interest rate credit cards, for example, often compound interest monthly. This means that if you are carrying a balance, the amount you have to pay back grows exponentially every month.

Calculate annual compound interest. Suppose you had a credit card on which you were carrying a $20,000 balance. The interest rate is 20 percent compounded annually. Calculate how much interest will accrue on the balance due in two years with the formula [ P ( 1 + i ) n ] − P {\displaystyle [P(1+i)^{n}]-P} [P(1+i)^{n}]-P. In this example, P = $20,000, i = .2 and n = 2. You would calculate [ $ 20 , 000 ( 1 + .2 ) 2 ] − $ 20 , 000 {\displaystyle [\$20,000(1+.2)^{2}]-\$20,000} [\$20,000(1+.2)^{2}]-\$20,000 ( $ 20 , 000 ∗ 1.44 ) − $ 20 , 000 {\displaystyle (\$20,000*1.44)-\$20,000} (\$20,000*1.44)-\$20,000 $ 28 , 800 − $ 20 , 000 = $ 8 , 800 {\displaystyle \$28,800-\$20,000=\$8,800} \$28,800-\$20,000=\$8,800. The total interest that would accrue would be $8,800, or an average of $367 per month.

Calculate interest compounded monthly on credit card debt. Suppose the interest on this credit card balance were compounded monthly instead of annually. You would use the formula [ P ( 1 + i / n ) n ∗ t ] − P {\displaystyle [P(1+i/n)^{n*t}]-P} [P(1+i/n)^{{n*t}}]-P. In this example, P = $20,000, i = .2, n = 12 and t = 2. Use the equation [ $ 20 , 000 ( 1 + .2 / 12 ) 12 ∗ 2 ] − $ 20 , 000 {\displaystyle [\$20,000(1+.2/12)^{12*2}]-\$20,000} [\$20,000(1+.2/12)^{{12*2}}]-\$20,000 ( $ 20 , 000 ∗ 1.49 ) − $ 20 , 000 {\displaystyle (\$20,000*1.49)-\$20,000} (\$20,000*1.49)-\$20,000 $ 29 , 738 − $ 20 , 000 = $ 9 , 738 {\displaystyle \$29,738-\$20,000=\$9,738} \$29,738-\$20,000=\$9,738. The total interest accrued on the credit card debt in two years would be $9,738, or an average of almost $406 per month.