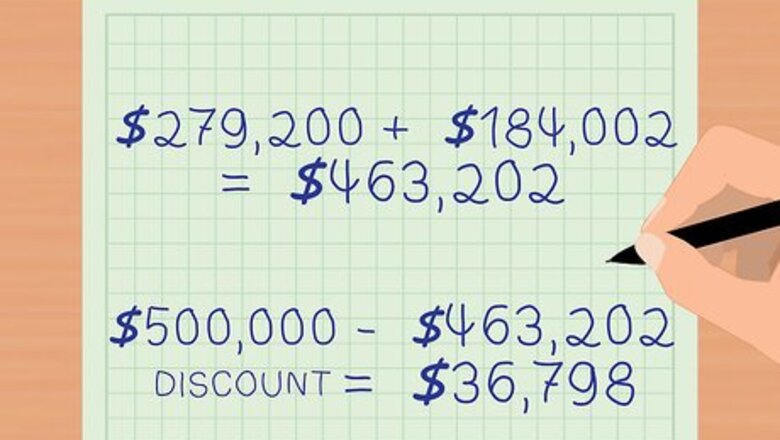
views
Calculating Interest for Bonds Sold at a Discount
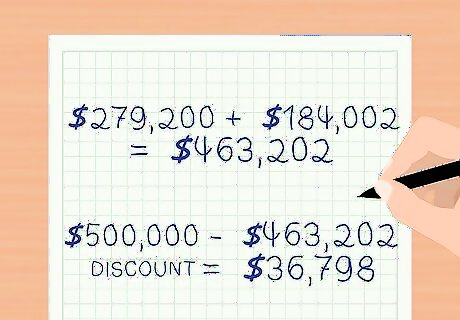
Determine the bond discount. If the market interest rate is higher than the coupon rate for the bond, then the bond must be sold at a discount. This means that the price of the bond is less than the face value, or par value of the bond. This compensates investors for the difference between the coupon rate and the market rate. For example, Company ABC issues 5-year, $500,000, 10 percent bonds, with interest paid semi-annually. The market interest rate is 12 percent, so the bond must be issued at a discount. The bond selling price equals the present value of the principal + the present value of the interest payments. The discount is the difference between the selling price and the face value of the bond. Interest is paid semi-annually, so the coupon rate per period is 5 percent (10 percent / 2) and the market interest rate per period is 6 percent (12 percent / 2). The number of periods is 10 (2 periods per year * 5 years). The coupon payment per period is $25,000 ($500,000 *.05). Calculate the present value of the principal. Multiply the face value of the bond by the present value interest factor (PVIF). Calculate PVIF with the formula 1 / ( 1 + r ) t {\displaystyle 1/(1+r)^{t}} 1/(1+r)^{t}, where r = the market interest rate per period and t = the number of periods. P V I F = 1 / ( 1 + .06 ) 1 0 = 0.5584 {\displaystyle PVIF=1/(1+.06)^{1}0=0.5584} PVIF=1/(1+.06)^{1}0=0.5584 Present value of the principal = $ 500 , 000 ∗ 0.5584 = $ 279 , 200 {\displaystyle \$500,000*0.5584=\$279,200} \$500,000*0.5584=\$279,200 Calculate the present value of the interest payments by multiplying the amount of the coupon payment by the present value factor for an ordinary annuity (PVOA). Calculate PVOA with the formula ( 1 − ( 1 / ( 1 + r ) t ) ) / r {\displaystyle (1-(1/(1+r)^{t}))/r} (1-(1/(1+r)^{t}))/r, where r = the market interest rate per period and t = the number of periods. P V O A = ( 1 − ( 1 / ( 1 + .06 ) 10 ) ) / .06 = 7.3601 {\displaystyle PVOA=(1-(1/(1+.06)^{10}))/.06=7.3601} PVOA=(1-(1/(1+.06)^{{10}}))/.06=7.3601 Multiply the amount of the coupon payment by the PVOA to get the present value of the interest. $ 25 , 000 ∗ 7.3601 = $ 184 , 002 {\displaystyle \$25,000*7.3601=\$184,002} \$25,000*7.3601=\$184,002. The selling price of the bond = the present value of the principal + the present value of the interest. $ 279 , 200 + $ 184 , 002 = $ 463 , 202 {\displaystyle \$279,200+\$184,002=\$463,202} \$279,200+\$184,002=\$463,202 The discount is $ 500 , 000 − $ 463 , 202 = $ 36 , 798 {\displaystyle \$500,000-\$463,202=\$36,798} \$500,000-\$463,202=\$36,798
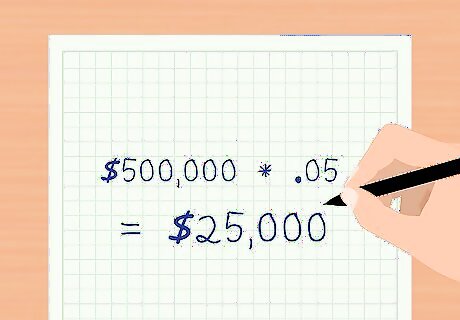
Calculate the interest payment for each period. The interest payment for each period is the amount the investor receives each period. This is the coupon payment * the face value of the bond. Using the above example, the coupon payment per period is 5 percent (10 percent / 2 payments per year = 5 percent). The face value of the bond is $500,000. $ 500 , 000 ∗ .05 = $ 25 , 000 {\displaystyle \$500,000*.05=\$25,000} \$500,000*.05=\$25,000. The interest payment per period is $25,000.
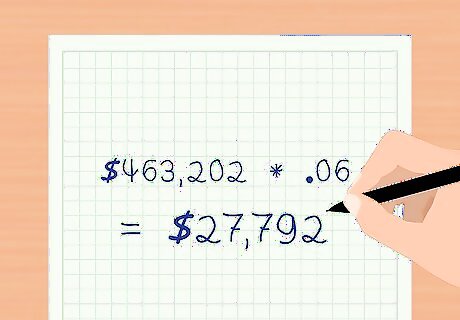
Compute the total effective interest expense for each period. Since you sold the bond at a discount, the effective interest rate you are paying on the bond equals the market interest rate at the time you issued the bond. The total interest expense is the present value of the bond * the effective interest rate. This gets recalculated every period. Using the above example, the present value of the bond on the date of issue is $463,202. The total interest expense is the present value * the effective interest rate per period. $ 463 , 202 ∗ .06 = $ 27 , 792 {\displaystyle \$463,202*.06=\$27,792} \$463,202*.06=\$27,792
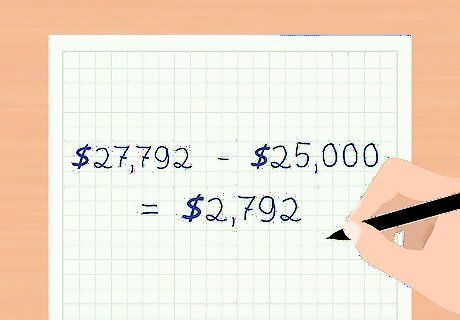
Record the interest paid and the amortization of the discount. Because you issued the bond at a discount, you paid an effective interest amount of $27,792. However, you have to separate out the amount of interest paid to investors and the amortization of the discount on your monthly financial statements. The total effective interest expense is $27,792. The coupon payment to investors is $25,000. The amortization expense of the discount for this period is $ 27 , 792 − $ 25 , 000 = $ 2 , 792 {\displaystyle \$27,792-\$25,000=\$2,792} \$27,792-\$25,000=\$2,792. On your financial statement for this month, record a debit of $27,792 to interest expense, a credit of $2,792 to Discount on Bonds Payable and a credit of $25,000 to Cash.
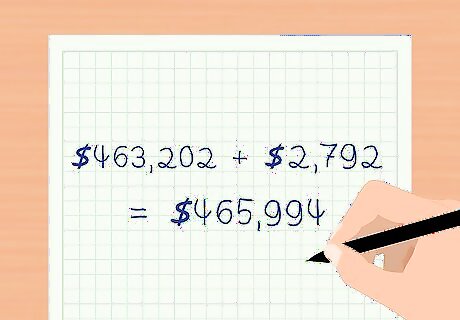
Verify the ending present value of the bond. Now you need to recalculate the present value of the bond. This will be the beginning present value of the bond from this period plus the amortization recorded for this period. You will use the ending present value from this period as the beginning present value for the next period when you recalculate the total interest expense. The beginning present value for the period was $463,202. The amortization of the discount for this period was $2,792. The ending present value for the period is $ 463 , 202 + $ 2 , 792 = $ 465 , 994 {\displaystyle \$463,202+\$2,792=\$465,994} \$463,202+\$2,792=\$465,994. Use $465,994 when as the beginning present value calculating the total effective interest expense for the next period.
Calculating Interest for Bonds Sold at a Premium

Determine the bond premium. If the market interest rate is lower than the coupon rate for the bond, then the bond must be sold at a premium. This means that the price of the bond is more than the face value, or par value of the bond. This is how investors compensate for the difference between the coupon rate and the market rate. For example, Company XYZ issues 5-year, $500,000, 10 percent bonds, with interest paid semi-annually. The market interest rate is 8 percent, so the bond must be issued at a premium. The bond selling price equals the present value of the principal + the present value of the interest payments. The premium is the difference between the selling price and the face value of the bond. Interest is paid semi-annually, so the coupon rate per period is 5 percent (10 percent / 2) and the market interest rate per period is 4 percent (8 percent / 2). The number of periods is 10 (2 periods per year * 5 years). The coupon payment per period is $25,000 ($500,000 *.05). Calculate the present value of the principal. Multiply the face value of the bond by the present value interest factor (PVIF). Calculate PVIF with the formula 1 / ( 1 + r ) t {\displaystyle 1/(1+r)^{t}} 1/(1+r)^{t}, where r = the market interest rate per period and t = the number of periods. P V I F = 1 / ( 1 + .04 ) 1 0 = 0.6756 {\displaystyle PVIF=1/(1+.04)^{1}0=0.6756} PVIF=1/(1+.04)^{1}0=0.6756 Present value of the principal = $ 500 , 000 ∗ 0.6756 = $ 337 , 800 {\displaystyle \$500,000*0.6756=\$337,800} \$500,000*0.6756=\$337,800 Calculate the present value of the interest payments by multiplying the amount of the coupon payment by the present value factor for an ordinary annuity (PVOA). Calculate PVOA with the formula ( 1 − ( 1 / ( 1 + r ) t ) ) / r {\displaystyle (1-(1/(1+r)^{t}))/r} (1-(1/(1+r)^{t}))/r, where r = the market interest rate per period and t = the number of periods. P V O A = ( 1 − ( 1 / ( 1 + .04 ) 10 ) ) / .06 = 8.1109 {\displaystyle PVOA=(1-(1/(1+.04)^{10}))/.06=8.1109} PVOA=(1-(1/(1+.04)^{{10}}))/.06=8.1109 Multiply the amount of the coupon payment by the PVOA to get the present value of the interest. $ 25 , 000 ∗ 8.1109 = $ 202 , 773 {\displaystyle \$25,000*8.1109=\$202,773} \$25,000*8.1109=\$202,773. The selling price of the bond = the present value of the principal + the present value of the interest. $ 337 , 800 + $ 202 , 773 = $ 540 , 573 {\displaystyle \$337,800+\$202,773=\$540,573} \$337,800+\$202,773=\$540,573 The premium is $ 540 , 573 − $ 500 , 000 = $ 40 , 573 {\displaystyle \$540,573-\$500,000=\$40,573} \$540,573-\$500,000=\$40,573
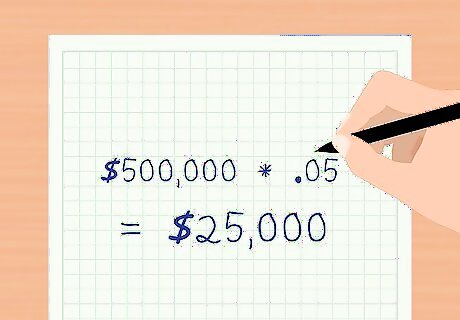
Calculate the interest payment for each period. The interest payment for each period is the amount the investor receives each period. This is the coupon payment * the face value of the bond. Using the above example, the coupon payment per period is 5 percent (10 percent / 2 payments per year = 5 percent). The face value of the bond is $500,000. $ 500 , 000 ∗ .05 = $ 25 , 000 {\displaystyle \$500,000*.05=\$25,000} \$500,000*.05=\$25,000. The interest payment per period is $25,000.
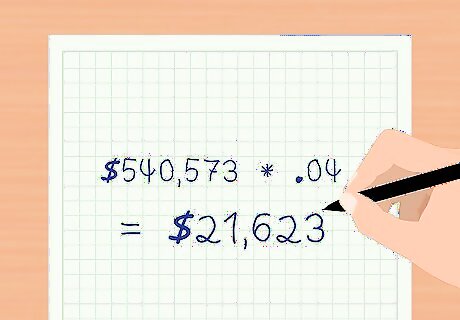
Compute the total effective interest expense for each period. Since you sold the bond at a premium, the effective interest rate you are paying on the bond equals the market interest rate at the time you issued the bond. The total interest expense is the present value of the bond * the effective interest rate. This gets recalculated every period. Using the above example, the present value of the bond on the date if issue is $540,573. The total interest expense is the present value * the effective interest rate per period. $ 540 , 573 ∗ .04 = $ 21 , 623 {\displaystyle \$540,573*.04=\$21,623} \$540,573*.04=\$21,623
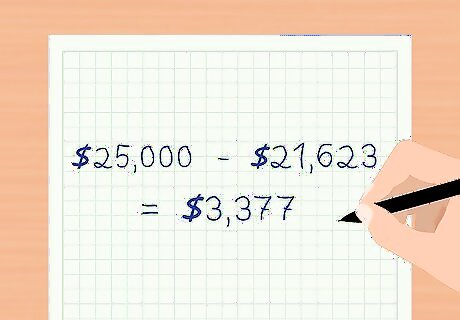
Record the interest paid and the amortization of the premium. Because you issued the bond at a premium, you paid an effective interest amount of $21,623. However, you have to separate out the amount of interest paid to investors and the amortization of the premium on your monthly financial statements. The total effective interest expense is $21,623. The coupon payment to investors is $25,000. The amortization expense of the premium for this period is $ 25 , 000 − 21 , 623 = $ 3 , 377 {\displaystyle \$25,000-21,623=\$3,377} \$25,000-21,623=\$3,377. On your financial statement for this month, record a debit of $21,623 to interest expense, a debit of $3,377 to Premium on Bonds Payable and a credit of $25,000 to Cash.
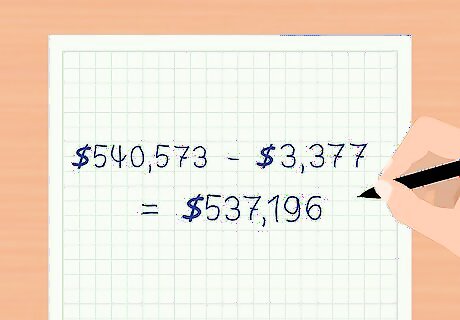
Verify the ending present value of the bond. Now you need to recalculate the present value of the bond. This will be the beginning present value of the bond from this period less the amortization recorded for this period. You will use the ending present value from this period as the beginning present value for the next period when you recalculate the total interest expense. The beginning present value for the period was $540,573. The amortization of the discount for this period was $3,377. The ending present value for the period is $ 540 , 573 − $ 3 , 3777 = $ 537 , 196 {\displaystyle \$540,573-\$3,3777=\$537,196} \$540,573-\$3,3777=\$537,196. Use $537,196 as the beginning present value when calculating the total effective interest expense for the next period.
Calculating Interest for Bonds Sold at Face Value

Gather the information. When a bond is sold at face value, or issued at par, the selling price equals the principal of the bond. Also, the yield, or the return, on the bond equals the interest rate. To calculate the annual interest, you need to know the coupon rate and the price of the bond. For example, Company QRS issues 5-year, $500,000, 10 percent bonds, with interest paid semi-annually. The market interest rate is 10 percent, so the bond is issued at par. Interest is paid semi-annually, so the coupon rate per period is 5 percent (10 percent / 2) and the market interest rate per period is 5 percent (10 percent / 2). The number of periods is 10 (2 periods per year * 5 years).
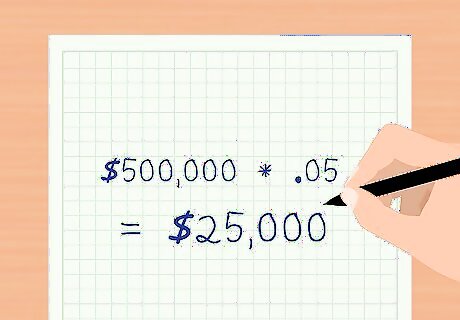
Calculate the interest payment for each period. Multiply the face value of the bond by the coupon rate per period. This tells you the interest payment the investors receive each period. Using the above example, the face value of the bond is $500,000 and the coupon rate per period is 5 percent. $ 500 , 000 ∗ .05 = $ 25 , 000 {\displaystyle \$500,000*.05=\$25,000} \$500,000*.05=\$25,000 The interest payment to investors each period is $25,000
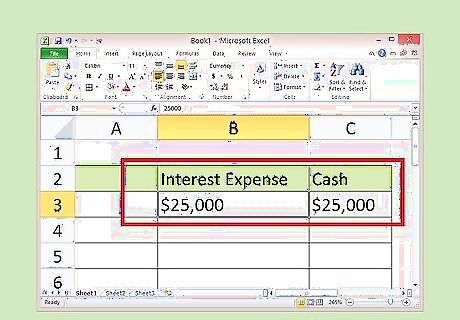
Record the total interest expense. Because you issued the bond at par, the journal entries are straightforward. You don’t need to record any amortization of discounts or premiums. For each period, record a debit of $25,000 to Interest Expense. Also, record a credit of $25,000 to Cash.



















Comments
0 comment