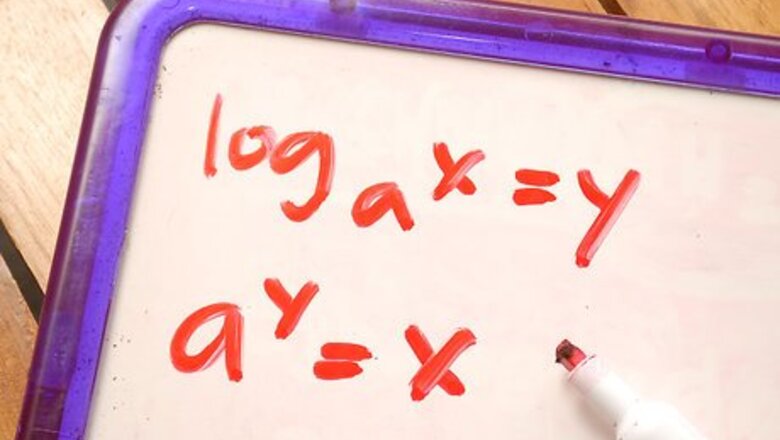
views
X
Research source
logax = y is the same as ay = x.

Know the difference between logarithmic and exponential equations. This is a very simple first step. If it contains a logarithm (for example: logax = y) it is logarithmic problem. A logarithm is denoted by the letters "log". If the equation contains an exponent (that is, a variable raised to a power) it is an exponential equation. An exponent is a superscript number placed after a number. Logarithmic: logax = y Exponential: a = x

Know the parts of a logarithm. The base is the subscript number found after the letters "log"--2 in this example. The argument or number is the number following the subscript number--8 in this example. Lastly, the answer is the number that the logarithmic expression is set equal to--3 in this equation.

Know the difference between a common log and a natural or Napierian log. Common logs have a base of 10. (for example, log10x). If a log is written without a base (as log x), then it is assumed to have a base of 10. Natural or Napierian logs: These are logs with a base of e. e is a mathematical constant that is equal to the limit of (1 + 1/n) as n approaches infinity, which is approximately equal to 2.718281828. The larger the value we plug in for n, the closer we get to 2.71828. It's important to understand that 2.71828 or e is not an exact value. You can think of it like the value of pi where there is an infinite number of digits after the decimal place. In other words, it's an irrational number that we round to 2.71828. Also, logex is often written as ln x. For example, ln 20 means the natural log of 20 and since the base of a natural log is e, or 2.71828, the value of the natural log of 20 is approximately equal to 3 because 2.71828 to the 3rd is approximately equal to 20. Note than you can find the natural log of 20 on your calculator using the LN button. Natural logs are critical for the advance study of math and science and you will learn more about their uses in future courses. For the time being however, it's important to become familiar with the basics of natural logarithms. Other Logs: Other logs have the base other than that of the common log and the E mathematical base constant. Binary logs have a base of 2 (for the example, log2x). Hexadecimal logs have the base of 16. Logs that have the 64 base are used in Advanced Computer Geometry (ACG) domain.

Know and apply the properties of logarithms. The properties of logarithms allow you to solve logarithmic and exponential equations that would be otherwise impossible. These only work if the base a and the argument are positive. Also the base a cannot be 1 or 0. The properties of logarithms are listed below with a separate example for each one with numbers instead of variables. These properties are for use when solving equations. loga(xy) = logax + logay A log of two numbers, x and y, that are being multiplied by each other can be split into two separate logs: a log of each of the factors being added together. (This also works in reverse.)Example:log216 =log28*2 =log28 + log22 loga(x/y) = logax - logayA log of two numbers being divided by each other, x and y, can be split into two logs: the log of the dividend x minus the log of the divisor y.Example:log2(5/3) = log25 - log23 loga(x) = r*logaxIf the argument x of the log has an exponent r, the exponent can be moved to the front of the logarithm.Example:log2(6)5*log26 loga(1/x) = -logaxThink about the argument. (1/x) is equal to x. Basically this is another version of the previous property.Example:log2(1/3) = -log23 logaa = 1If the base a equals the argument a the answer is 1. This is very easy to remember if one thinks about the logarithm in exponential form. How many times should one multiply a by itself to get a? Once.Example:log22 = 1 loga1 = 0If the argument is one the answer is always zero. This property holds true because any number with an exponent of zero is equal to one.Example:log31 =0 (logbx/logba) = logaxThis is known as "Change of Base". One log divided by another, both with the same base b, is equal to a single log. The argument a of the denominator becomes the new base, and the argument x of the numerator becomes the new argument. This is easy to remember if you think about the base as the bottom of an object and the denominator as the bottom of a fraction.Example:log25 = (log 5/log 2)
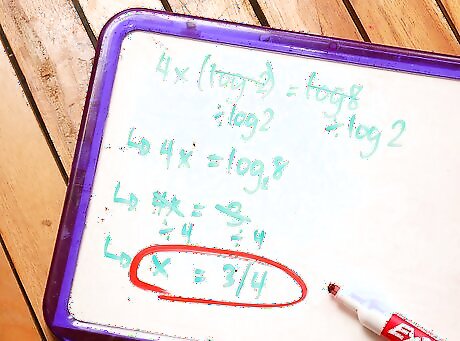
Practice using the properties. These properties are best memorized by repeated use when solving equations. Here's an example of an equation that is best solved with one of the properties:4x*log2 = log8 Divide both sides by log2.4x = (log8/log2) Use Change of Base.4x = log28 Compute the value of the log.4x = 3 Divide both sides by 4. x = 3/4 Solved. This is very helpful. I now understand logs.
















Comments
0 comment