views
Define Terms
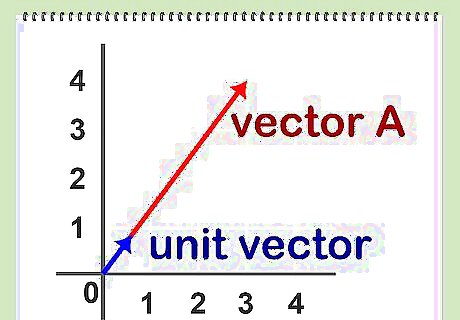
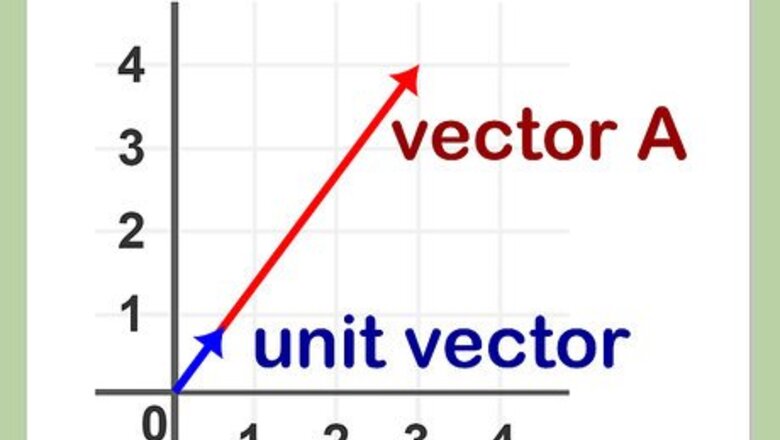
Define a unit vector. The unit vector of a vector A is the vector with the same initial point and direction as A, but with a length of 1 unit. It can be mathematically proven that there is one and only one unit vector for each given vector A.
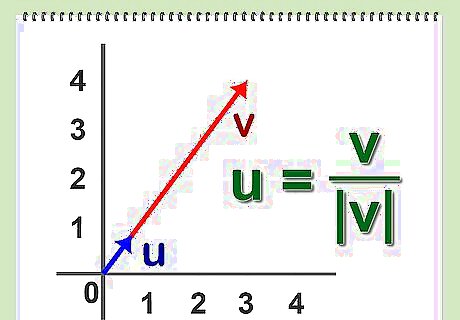
Define the Normalization of a vector. This is the process of identifying the unit vector for a given vector A.
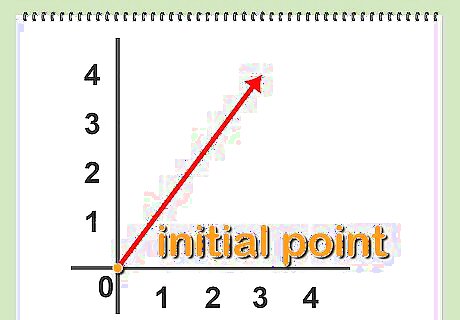
Define a bound vector. A bound vector in Cartesian space has its initial point at the origin of the coordinate system, expressed as (0,0) in two dimensions. This allows you to identify a vector solely in terms of its terminal point.
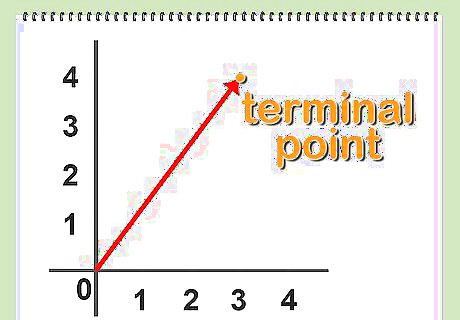
Describe vector notation. By restricting ourselves to bound vectors, A = (x, y) where the coordinate pair (x,y) indicates the location of the terminal point for vector A.
Analyze the Objective
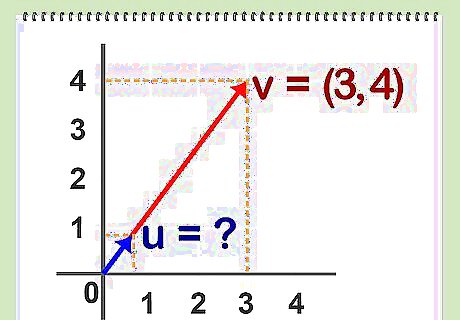
Establish the known values. From the definition of the unit vector, we know that the initial point and direction of the unit vector is the same as the given vector A. Furthermore, we know the length of the unit vector is 1.
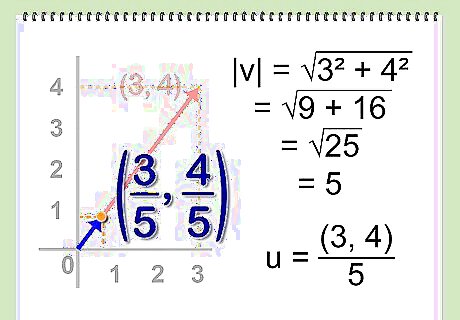
Determine the unknown value. The only variable we need to calculate is the terminal point of the unit vector.


















Comments
0 comment