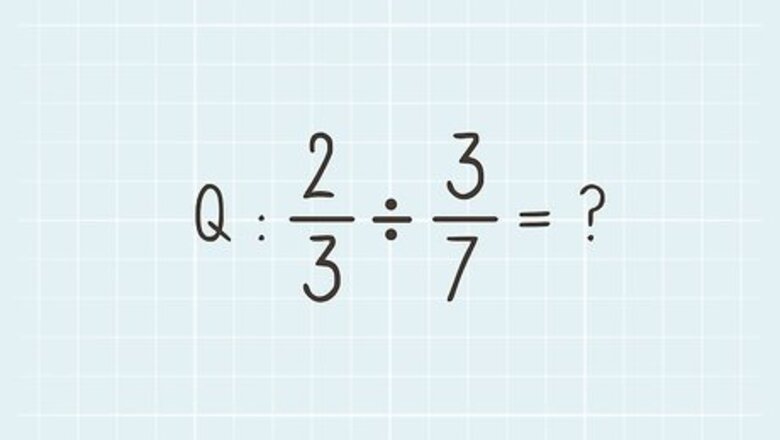
views
X
Expert Source
David JiaAcademic Tutor
Expert Interview. 7 January 2021.
This article will guide you through the process and show you that dividing fractions by fractions is really a breeze.
Dividing Fractions by Fractions (Example)
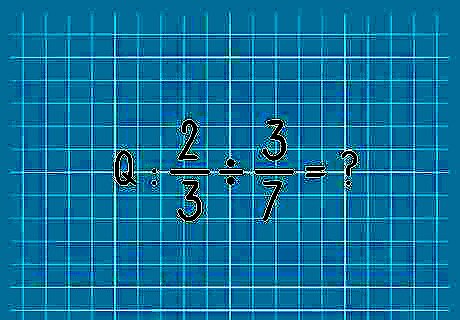
Begin with an example problem. Let's use 2/3 ÷ 3/7. This question is asking us how many parts equal to 3/7 of a whole can be found in the value 2/3. Don't worry; it's not as hard as it sounds!

Change the division sign to a multiplication sign. Your new equation should read: 2/3 * __ (we'll fill in the blank in a moment.)

Now find the reciprocal of the second fraction. This means flipping 3/7 over so that the numerator (3) is now on the bottom, and the denominator (7) is now on the top. The reciprocal of 3/7 is 7/3. Now write out your new equation: 2/3 * 7/3 = __

Multiply your fractions. First multiply the numerators of the two fractions together: 2 * 7 = 14. 14 is the numerator (top value) of your answer. Then multiply the denominators of the two fractions together: 3 * 3 = 9. 9 is the denominator (bottom value) of your answer. You now know that 2/3 * 7/3 = 14/9.
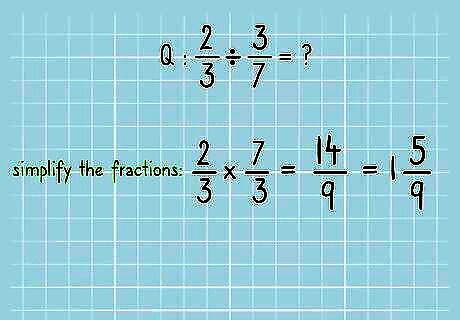
Simplify your fraction. In this case, because the numerator of the fraction is larger than the denominator, we know that our fraction is larger than 1, and we should convert it to a mixed fraction. (A mixed fraction is a whole number and a fraction combined, like 1 2/3). First divide the numerator 14 by 9. 9 goes into 14 one time, with a remainder of 5, so you should write out your reduced fraction out as: 1 5/9 (“one and five ninths”). Stop there, you have found your answer! You can determine that you cannot reduce the fraction further because the denominator is not evenly divisible by the numerator (9 cannot be divided evenly by 5) and the numerator is a prime number, or an integer that can only be divisible by one and itself. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To simplify fractions, you can divide both the numerator and denominator by a common factor. This creates a new, easier-to-use fraction with smaller components, but it represents the same value. For instance, if you divide both the numerator and denominator of 6/12 by 2, you get 3/6, which is equal to 1/2.

Try another example! Let's try the problem 4/5 ÷ 2/6 =. First change the division sign to a multiplication sign (4/5 * __ = ), then find the reciprocal of 2/6, which is 6/2. You know have the equation: 4/5 * 6/2 =__. Now multiply the numerators, 4 * 6 = 24, and the denominators 5* 2 = 10. You now have4/5 * 6/2 = 24/10. Now simplify the fraction. Because the numerator is larger than the denominator, we will need to convert this to a mixed fraction. First divide the numerator by the denominator, (24/10 = 2 remainder 4). Write the answer out as 2 4/10. We could still reduce this fraction further! Note that 4 and 10 are both even numbers, so the first step in reducing them is to divide them each by 2. We end up with 2/5. Because the denominator (5) cannot be divided evenly by the numerator (2), and it is a prime number, we know that it cannot be reduced further. Our answer is thus: 2 2/5.

Get additional help with reducing fractions. You probably spent a lot of time learning to reduce fractions before trying to divide them by each other, but if you need a refresher or some more help, there are some great articles online that can help you a lot.
Understanding How to Divide Fractions by Fractions
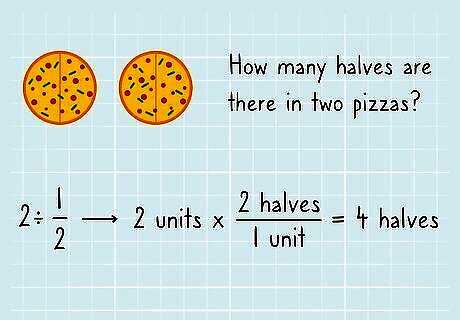
Think about what dividing by a fraction means. The problem 2 ÷ 1/2 is asking you: ”How many halves are in 2?” The answer is 4, because each unit (1) is made up of two halves, and there are 2 units total: 2 halves/1 unit * 2 units = 4 halves. Try thinking about this same equation in terms of cups of water: How many half cups of water are in 2 cups of water? You could pour 2 half cups of water into each cup of water which means you are basically adding them, and you have two cups: 2 halves/1 cup * 2 cups = 4 halves. All of this means that when the fraction you are dividing by is between 0 and 1, the answer will always be larger than the original number! This is true whether you are dividing whole numbers or fractions by a fraction.

Understand that dividing is the opposite of multiplying. Therefore, dividing by a fraction can be accomplished by multiplying by its reciprocal. The reciprocal of a fraction (also called its “multiplicative inverse”) is just the fraction turned upside down, so that the numerator and denominator have switched places. In a moment, we are going to divide fractions by fractions by finding the reciprocal of the second fraction and multiplying them together, but let's look at some reciprocals first: The reciprocal of 3/4 is 4/3. The reciprocal of 7/5 is 5/7. The reciprocal of 1/2 is 2/1, or 2.

Memorize the following steps for dividing a fraction by a fraction. In order, the steps are: Leave the first fraction in the equation alone. Turn the division sign into a multiplication sign. Flip the second fraction over (find its reciprocal). Multiply the numerators (top numbers) of the two fractions together. This result will be the numerator (top portion) of your answer. Multiply the denominators (bottom numbers) of the two fractions together. The result will be the denominator of your answer. Simplify your fraction by reducing it to the simplest terms.

Work through these steps on the example 1/3 ÷ 2/5. We will begin by leaving the first fraction alone, and changing the division sign to a multiplication sign: 1/3 ÷ 2/5 = becomes: 1/3 * __ = Now we flip the second fraction (2/5) over to find its reciprocal, 5/2: 1/3 * 5/2 = Now multiply the numerators (top numbers) of the two fractions, 1*5 = 5. 1/3 * 5/2 = 5/ Now multiply the denominators (bottom numbers) of the two fractions, 3*2 = 6. We now have: 1/3 * 5/2 = 5/6 This particular fraction cannot be simplified further, so we have our answer.

Try remembering the following rhyme to help you remember: "Dividing fractions, as easy as pie, Flip the second fraction, then multiply. And don't forget to simplify, Before it's time to say goodbye." Another helpful saying that tells you what to do with each part of the equation is: “Leave Me (the first fraction), Change Me (the division symbol), Turn Me Over (the second fraction).”


















Comments
0 comment