views
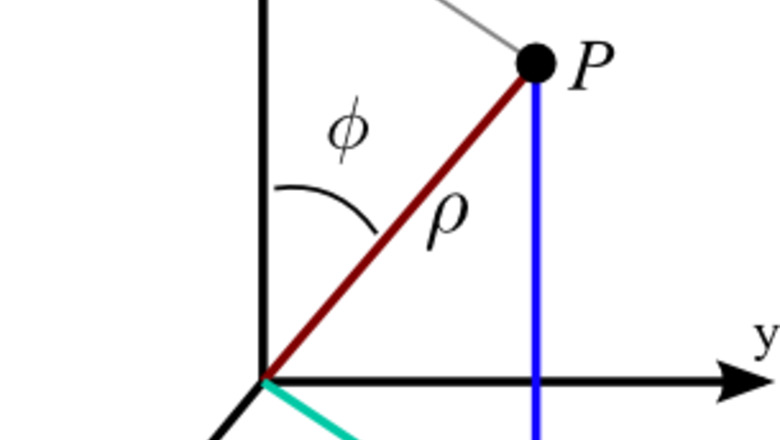
This article will use the mathematician's convention of labeling coordinates
(
ρ
,
θ
,
ϕ
)
,
{\displaystyle (\rho ,\theta ,\phi ),}
where
ρ
{\displaystyle \rho }
is the radial distance,
θ
{\displaystyle \theta }
is the azimuthal angle, and
ϕ
{\displaystyle \phi }
is the polar angle. In physics, the angles are switched (but are still written out in that order).
Steps
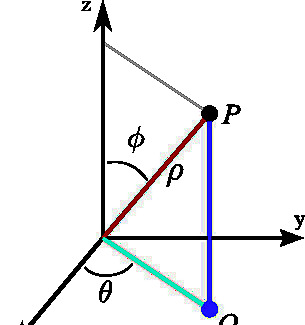
Recall the coordinate conversions. Coordinate conversions exist from Cartesian to spherical and from cylindrical to spherical. Below is a list of conversions from Cartesian to spherical. Above is a diagram with point P {\displaystyle P} P described in spherical coordinates. x = ρ sin ϕ cos θ y = ρ sin ϕ sin θ z = ρ cos ϕ ρ 2 = x 2 + y 2 + z 2 {\displaystyle {\begin{aligned}x&=\rho \sin \phi \cos \theta \\y&=\rho \sin \phi \sin \theta \\z&=\rho \cos \phi \\\rho ^{2}&=x^{2}+y^{2}+z^{2}\end{aligned}}} {\begin{aligned}x&=\rho \sin \phi \cos \theta \\y&=\rho \sin \phi \sin \theta \\z&=\rho \cos \phi \\\rho ^{{2}}&=x^{{2}}+y^{{2}}+z^{{2}}\end{aligned}} In the example where we calculate the moment of inertia of a ball, x 2 + y 2 = ρ 2 sin 2 ϕ {\displaystyle x^{2}+y^{2}=\rho ^{2}\sin ^{2}\phi } x^{{2}}+y^{{2}}=\rho ^{{2}}\sin ^{{2}}\phi will be useful. Make sure you know why this is the case.
Set up the coordinate-independent integral. We are dealing with volume integrals in three dimensions, so we will use a volume differential d V {\displaystyle \mathrm {d} V} {\mathrm {d}}V and integrate over a volume V . {\displaystyle V.} V. ∫ V d V {\displaystyle \int _{V}\mathrm {d} V} \int _{{V}}{\mathrm {d}}V Most of the time, you will have an expression in the integrand. If so, make sure that it is in spherical coordinates.
Set up the volume element. d V = ρ 2 sin ϕ d ρ d ϕ d θ {\displaystyle \mathrm {d} V=\rho ^{2}\sin \phi \mathrm {d} \rho \mathrm {d} \phi \mathrm {d} \theta } {\mathrm {d}}V=\rho ^{{2}}\sin \phi {\mathrm {d}}\rho {\mathrm {d}}\phi {\mathrm {d}}\theta Those familiar with polar coordinates will understand that the area element d A = r d r d θ . {\displaystyle \mathrm {d} A=r\mathrm {d} r\mathrm {d} \theta .} {\mathrm {d}}A=r{\mathrm {d}}r{\mathrm {d}}\theta . This extra r stems from the fact that the side of the differential polar rectangle facing the angle has a side length of r d θ {\displaystyle r\mathrm {d} \theta } r{\mathrm {d}}\theta to scale to units of distance. A similar thing is occurring here in spherical coordinates.
Set up the boundaries. Choose a coordinate system that allows for the easiest integration. Notice that ϕ {\displaystyle \phi } \phi has a range of [ 0 , π ] , {\displaystyle [0,\pi ],} [0,\pi ], not [ 0 , 2 π ] . {\displaystyle [0,2\pi ].} [0,2\pi ]. This is because θ {\displaystyle \theta } \theta already has a range of [ 0 , 2 π ] , {\displaystyle [0,2\pi ],} [0,2\pi ], so the range of ϕ {\displaystyle \phi } \phi ensures that we don't integrate over a volume twice.
Integrate. Once everything is set up in spherical coordinates, simply integrate using any means possible and evaluate.
Moment of Inertia of a Ball
Calculate the moment of inertia of a ball. Assume this ball has a mass M , {\displaystyle M,} M, radius R , {\displaystyle R,} R, and a constant density σ . {\displaystyle \sigma .} \sigma . Most moment of inertia questions are written with answers in terms of M {\displaystyle M} M and R . {\displaystyle R.} R.
Recall the moment of inertia formula. I = ∫ M r 2 d m , {\displaystyle I=\int _{M}r^{2}\mathrm {d} m,} I=\int _{{M}}r^{{2}}{\mathrm {d}}m, where r = x 2 + y 2 {\displaystyle r={\sqrt {x^{2}+y^{2}}}} r={\sqrt {x^{{2}}+y^{{2}}}} is the perpendicular distance from the axis (we are choosing the z-axis) and we are integrating over the mass M . {\displaystyle M.} M.
Recall the relationship between mass, volume, and density when density is constant. σ = M V . {\displaystyle \sigma ={\frac {M}{V}}.} \sigma ={\frac {M}{V}}. Of course, we know the volume of the sphere, so σ = 3 M 4 π R 3 . {\displaystyle \sigma ={\frac {3M}{4\pi R^{3}}}.} \sigma ={\frac {3M}{4\pi R^{{3}}}}.
Rewrite the moment of inertia in terms of a volume integral, then solve. Note constants that factor out. d m = σ d V , {\displaystyle \mathrm {d} m=\sigma \mathrm {d} V,} {\mathrm {d}}m=\sigma {\mathrm {d}}V, so therefore, I z = ∫ V ( x 2 + y 2 ) 3 M 4 π R 3 d V = 3 M 4 π R 3 ∫ 0 R ρ 2 d ρ ∫ 0 π sin ϕ d ϕ ∫ 0 2 π d θ ρ 2 sin 2 ϕ = 3 M 4 π R 3 ∫ 0 R ρ 4 d ρ ∫ 0 π sin 3 ϕ d ϕ ∫ 0 2 π d θ = 3 M 4 π R 3 ( 1 5 R 5 ) ( 2 π ) ∫ 0 π ( 1 − cos 2 ϕ ) sin ϕ d ϕ , u = cos ϕ = 3 10 M R 2 ∫ − 1 1 ( 1 − u 2 ) d u = 3 10 M R 2 ( 2 ) ( 1 − 1 3 ) = 2 5 M R 2 {\displaystyle {\begin{aligned}I_{z}&=\int _{V}(x^{2}+y^{2}){\frac {3M}{4\pi R^{3}}}\mathrm {d} V\\&={\frac {3M}{4\pi R^{3}}}\int _{0}^{R}\rho ^{2}\mathrm {d} \rho \int _{0}^{\pi }\sin \phi \mathrm {d} \phi \int _{0}^{2\pi }\mathrm {d} \theta \rho ^{2}\sin ^{2}\phi \\&={\frac {3M}{4\pi R^{3}}}\int _{0}^{R}\rho ^{4}\mathrm {d} \rho \int _{0}^{\pi }\sin ^{3}\phi \mathrm {d} \phi \int _{0}^{2\pi }\mathrm {d} \theta \\&={\frac {3M}{4\pi R^{3}}}\left({\frac {1}{5}}R^{5}\right)(2\pi )\int _{0}^{\pi }(1-\cos ^{2}\phi )\sin \phi \mathrm {d} \phi ,u=\cos \phi \\&={\frac {3}{10}}MR^{2}\int _{-1}^{1}(1-u^{2})\mathrm {d} u\\&={\frac {3}{10}}MR^{2}(2)\left(1-{\frac {1}{3}}\right)\\&={\frac {2}{5}}MR^{2}\end{aligned}}} {\begin{aligned}I_{{z}}&=\int _{{V}}(x^{{2}}+y^{{2}}){\frac {3M}{4\pi R^{{3}}}}{\mathrm {d}}V\\&={\frac {3M}{4\pi R^{{3}}}}\int _{{0}}^{{R}}\rho ^{{2}}{\mathrm {d}}\rho \int _{{0}}^{{\pi }}\sin \phi {\mathrm {d}}\phi \int _{{0}}^{{2\pi }}{\mathrm {d}}\theta \rho ^{{2}}\sin ^{{2}}\phi \\&={\frac {3M}{4\pi R^{{3}}}}\int _{{0}}^{{R}}\rho ^{{4}}{\mathrm {d}}\rho \int _{{0}}^{{\pi }}\sin ^{{3}}\phi {\mathrm {d}}\phi \int _{{0}}^{{2\pi }}{\mathrm {d}}\theta \\&={\frac {3M}{4\pi R^{{3}}}}\left({\frac {1}{5}}R^{{5}}\right)(2\pi )\int _{{0}}^{{\pi }}(1-\cos ^{{2}}\phi )\sin \phi {\mathrm {d}}\phi ,u=\cos \phi \\&={\frac {3}{10}}MR^{{2}}\int _{{-1}}^{{1}}(1-u^{{2}}){\mathrm {d}}u\\&={\frac {3}{10}}MR^{{2}}(2)\left(1-{\frac {1}{3}}\right)\\&={\frac {2}{5}}MR^{{2}}\end{aligned}} Note that in the step where the integral is written in terms of u , {\displaystyle u,} u, the integrand is an even function. Therefore, we can factor out a 2 and set the lower boundary to 0 to simplify calculations.














Comments
0 comment