views
Graphing the Basic Equations
Draw a coordinate plane. For a sine or cosine graph, simply go from 0 to 2π on the x-axis, and -1 to 1 on the y-axis, intersecting at the origin (0, 0). Both y = sin ( x ) {\displaystyle y=\sin(x)} y=\sin(x) and y = cos ( x ) {\displaystyle y=\cos(x)} y=\cos(x) repeat the same shape from negative infinity to positive infinity on the x-axis (you'll generally only graph a portion of it). Use the basic equations as given: y = sin ( x ) {\displaystyle y=\sin(x)} y=\sin(x) and y = c o s ( x ) {\displaystyle y=cos(x)} y=cos(x)
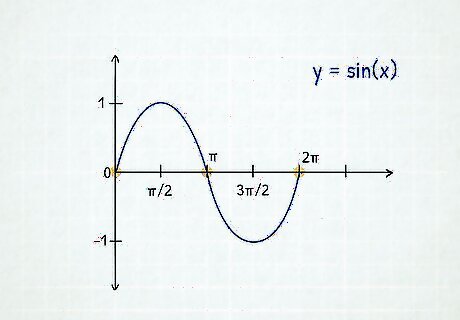
Graph the basic form of y = sin ( x ) {\displaystyle y=\sin(x)} y=\sin(x). Plot and connect the points (0, 0), (π/2, 1), (π, 0), and (3π/2, -1) with a continuous curve. Both y = sin ( x ) {\displaystyle y=\sin(x)} y=\sin(x) and y = cos ( x ) {\displaystyle y=\cos(x)} y=\cos(x) never go past -1 or 1 on the y-axis. Since you are only hand-drawing your graphs, there is no precise scale, but it must be accurate at certain points.
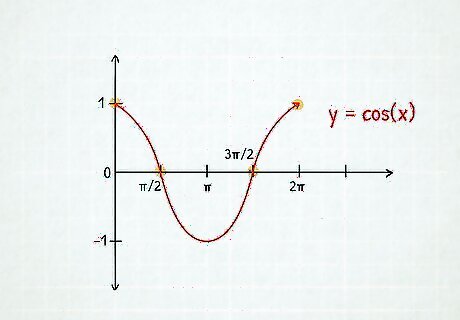
Graph the basic form of y = c o s ( x ) {\displaystyle y=cos(x)} y=cos(x). Plot and connect the points (0, 1), (π/2, 0), (π, -1), and (3π/2, 0) with a continuous curve. It may be helpful to use two separate colors to distinguish between sine and cosine. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Develop strong graphing skills. Drawing graphs by hand will help you develop foundational graphing skills, especially in understanding scales and axes. This will build a strong base for you to use helpful online tools to visualize complex relationships, perform calculations, and prepare for standardized tests.
Graphing Different Sine Equations

Use the standard equation to define your variables. y = A sin ( B x + C ) + D {\displaystyle y=A\sin(Bx+C)+D} y=A\sin(Bx+C)+D Find your values of A, B, C, and D. Note that in the basic equation for sine, A = 1, B = 1, C = 0, and D = 0.
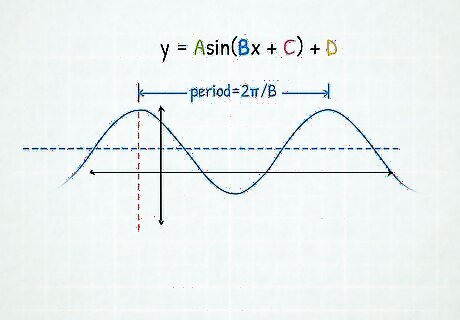
Calculate the period. Divide your period on the x-axis into four sections that are equal distances apart, just like in the basic equations. The y-values will still alternate from 0, 1, 0, and -1 just like in the basic equation. Period = 2 π B {\displaystyle {\text{Period}}={\frac {2\pi }{B}}} {\text{Period}}={\frac {2\pi }{B}}
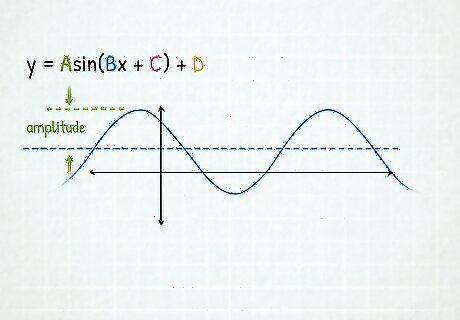
Calculate the amplitude. Amplitude = A {\displaystyle {\text{Amplitude}}=A} {\text{Amplitude}}=A Multiply the y-values you have by A, and graph these new points. If A is negative, the graph will flip over the x-axis. This is called a reflection.
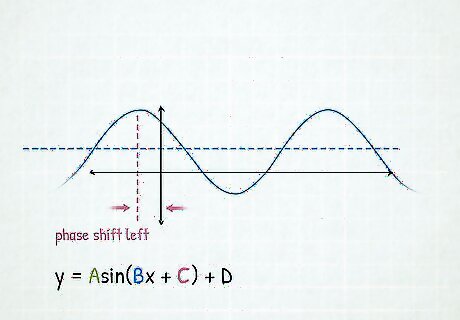
Calculate the phase shift. Phase shift = C B {\displaystyle {\text{Phase shift}}={\frac {C}{B}}} {\text{Phase shift}}={\frac {C}{B}} This will move the graph to the left or right. For each x-value in the period, move the x-value to the left by C/B if C/B is negative, or move each x-value to the right by C/B if C/B is positive.
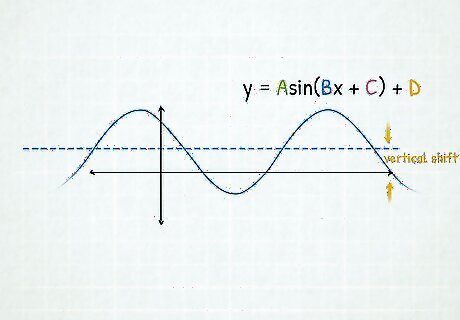
Calculate the vertical shift. Vertical shift = D {\displaystyle {\text{Vertical shift}}=D} {\text{Vertical shift}}=D For each y-value, move the y-value up by D if D is positive, or move the y-value down if D is negative.
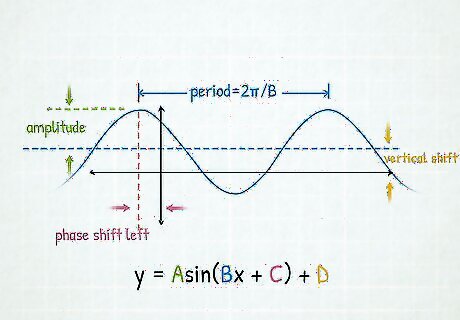
Graph the final function. After each transformation has been applied, your graph is finished! I.M. Gelfand I.M. Gelfand, Mathematician To accurately sketch sine and cosine curves, first mark the key points where y=0 or y=±1 based on their values at special angles on the unit circle. Connect those anchor points smoothly, minding the amplitude, period, phase shifts or compressions introduced by the function's coefficients. The intrinsic symmetry and cyclic nature of the waves emerges beautifully when following this methodical approach.
Graphing Different Cosine Equations

Use the standard equation to define your variables. y = A cos ( B x + C ) + D {\displaystyle y=A\cos(Bx+C)+D} y=A\cos(Bx+C)+D Find your values of A, B, C, and D. Note that in the basic equation for cosine, A = 1, B = 1, C = 0, and D = 0.
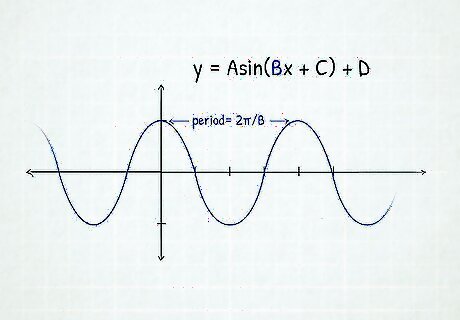
Calculate the period. Divide your period on the x-axis into four sections that are equal distances apart, just like in the basic equations. The y-values will still alternate from 1, 0, -1, and 0 just like in the basic equation. Period = 2 π B {\displaystyle {\text{Period}}={\frac {2\pi }{B}}} {\text{Period}}={\frac {2\pi }{B}}
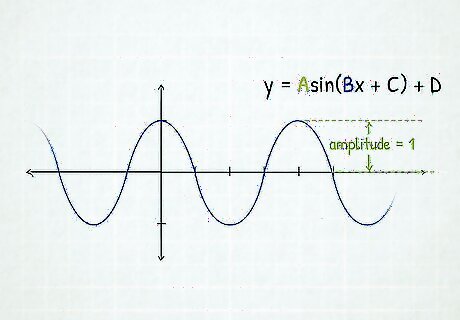
Calculate the amplitude. Amplitude = A {\displaystyle {\text{Amplitude}}=A} {\text{Amplitude}}=A Multiply the y-values you have by A, and graph these new points. If A is negative, the graph will flip over the x-axis. This is called a reflection.
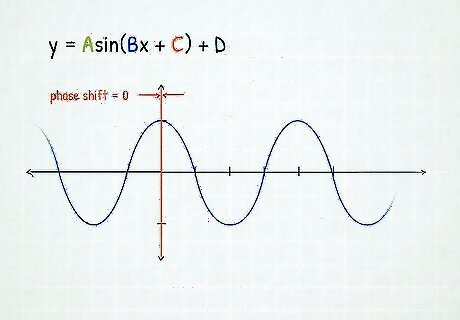
Calculate the phase shift. Phase shift = C B {\displaystyle {\text{Phase shift}}={\frac {C}{B}}} {\text{Phase shift}}={\frac {C}{B}} This will move the graph to the left or right. For each x-value in the period, move the x-value to the left by C/B if C/B is negative, or move each x-value to the right by C/B if C/B is positive.
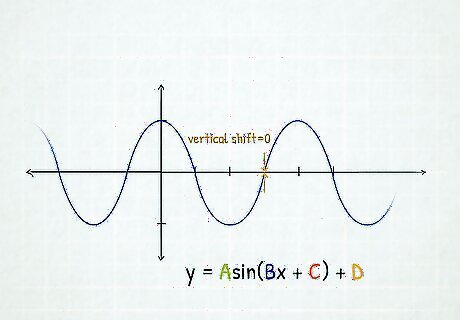
Calculate the vertical shift. Vertical shift = D {\displaystyle {\text{Vertical shift}}=D} {\text{Vertical shift}}=D This will move the graph up or down. For each y-value, move the y-value up by D if D is positive, or move the y-value down if D is negative.
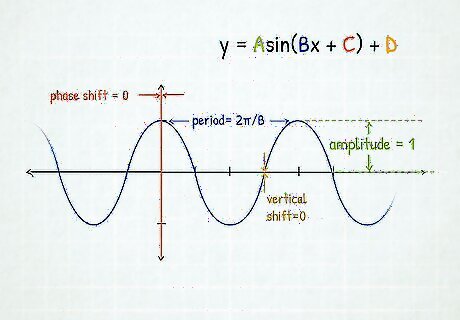
Graph the final function. After each transformation has been applied, your graph is finished!


















Comments
0 comment