views
Solving Absolute Value

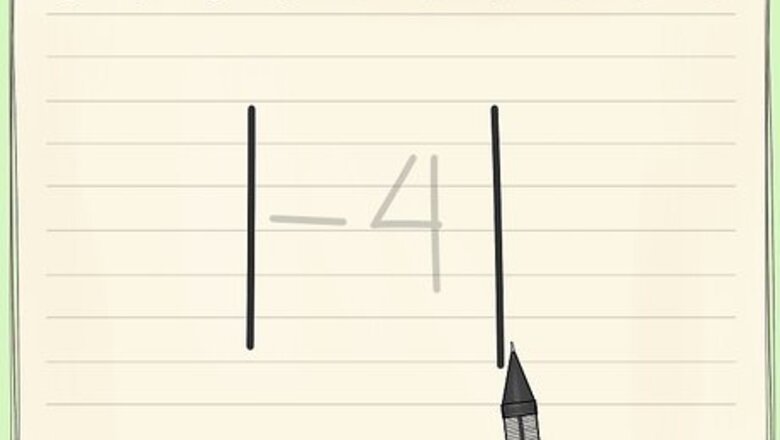
Remember that absolute value is a number's distance from zero. An absolute value is the distance from the number to zero along a number line. Simply put, | − 4 | {\displaystyle |-4|} |-4| is just asking you how far away -4 is from zero. Since distance is always a positive number (you can't travel "negative" steps, just steps in a different direction), the result of absolute value is always positive.

Make the number in the absolute value sign positive. At its most simple, absolute value makes any number positive. It is useful for measuring distance, or finding values in finances where you work with negative numbers like debt or loans.
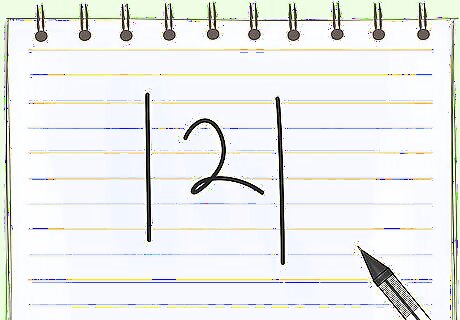
Use simple, vertical bars to show absolute value. The notation for absolute value is easy. Single bars (or a "pipe" on a keyboard, found near the enter key) around a number or expression, like | n | , | 3 + 5 | , | − 72 | {\displaystyle |n|,|3+5|,|-72|} |n|,|3+5|,|-72|, indicates absolute value. | 2 | {\displaystyle |2|} |2| is read as "the absolute value of 2."
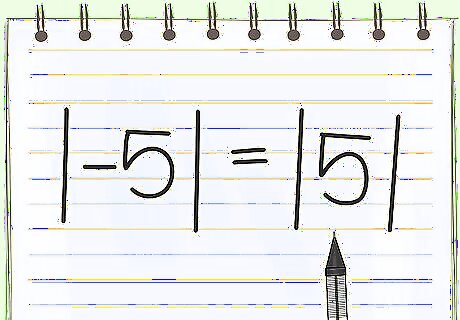
Drop any negative signs on the number inside the absolute value marks. For instance, |-5| would become |5|.
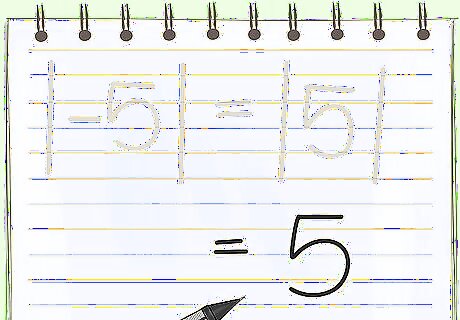
Drop the absolute value marks. The number remaining is your answer, so |-5| becomes |5| and then 5. This is all you need to do | − 5 | = 5 {\displaystyle |-5|=5} |-5|=5
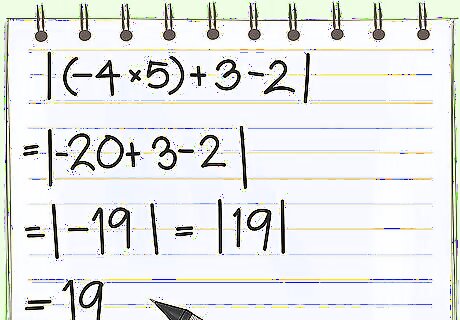
Simplify the expression inside the absolute value sign. If you've got a simple expression, like | − 10 | {\displaystyle |-10|} |-10|, you can just make the whole thing positive. But expressions like | ( − 4 ∗ 5 ) + 3 − 2 | {\displaystyle |(-4*5)+3-2|} |(-4*5)+3-2| need to be simplified before you can take the absolute value. The normal order of operations still applies: Problem: | ( − 4 ∗ 5 ) + 3 − 2 | {\displaystyle |(-4*5)+3-2|} |(-4*5)+3-2| Simplify inside parenthesis: | ( − 20 ) + 3 − 2 | {\displaystyle |(-20)+3-2|} |(-20)+3-2| Add and Subtract: | − 19 | {\displaystyle |-19|} |-19| Make everything inside the absolute value positive: | 19 | {\displaystyle |19|} |19| Final Answer: 19
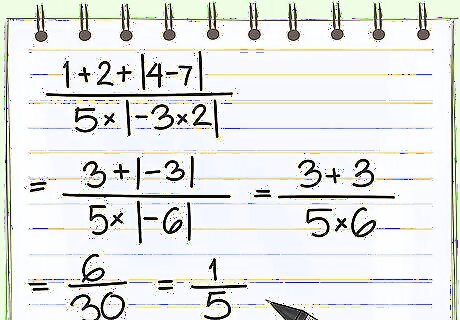
Always use the order of operations before finding absolute value. When determining longer equations, you want to do all the possible work before finding the absolute value. You should not simplify absolute values until everything else has been added, subtracted, and divided successfully. For example: Problem: 1 + 2 + | 4 − 7 | 5 ∗ | − 3 ∗ 2 | {\displaystyle {\frac {1+2+|4-7|}{5*|-3*2|}}} {\frac {1+2+|4-7|}{5*|-3*2|}} Perform the order of operations inside and outside the absolute value: 3 + | − 3 | 5 ∗ | − 6 | {\displaystyle {\frac {3+|-3|}{5*|-6|}}} {\frac {3+|-3|}{5*|-6|}} Take the absolute values: 3 + ( 3 ) 5 ∗ ( 6 ) {\displaystyle {\frac {3+(3)}{5*(6)}}} {\frac {3+(3)}{5*(6)}} Order of operations: 6 30 {\displaystyle {\frac {6}{30}}} {\frac {6}{30}} Simplify to final answer: 1 5 {\displaystyle {\frac {1}{5}}} {\frac {1}{5}}
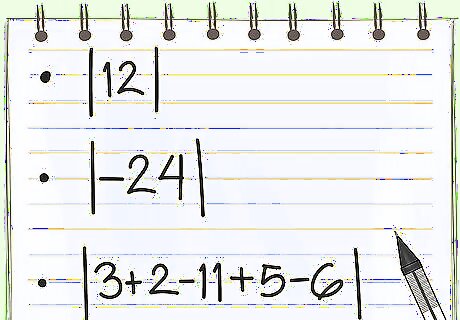
Keep working on some practice problems to get it down. Absolute value is pretty easy, but that doesn't mean a few practice problems won't help you keep the knowledge: | 12 | {\displaystyle |12|} |12| = 12 {\displaystyle 12} 12 | − 24 | {\displaystyle |-24|} |-24| = 24 {\displaystyle 24} 24 | 3 + 2 − 11 + 5 − 6 | {\displaystyle |3+2-11+5-6|} |3+2-11+5-6| = 7 {\displaystyle 7} 7
Solving Non-Real Absolute Values (Equations with "i")
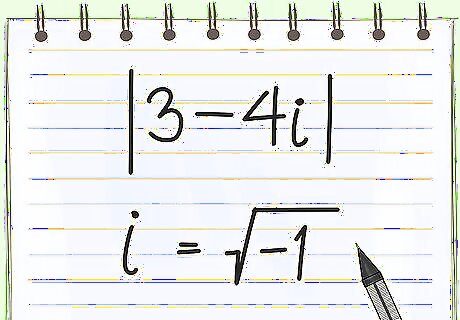
Note any complex equations with imaginary numbers, like "i" or − 1 {\displaystyle {\sqrt {-1}}} {\sqrt {-1}} and solve separately. You cannot find the absolute value of imaginary numbers the same way you found it for rational numbers. That said, you can easily find the absolute value of a complex equation by plugging it into the distance formula. Take the expression | 3 − 4 i | {\displaystyle |3-4i|} |3-4i|, for example. Problem: | 3 − 4 i | {\displaystyle |3-4i|} |3-4i| Note: If you see the expression − 1 {\displaystyle {\sqrt {-1}}} {\sqrt {-1}}, you can replace it with "i." The square root of -1 is an imaginary number, known as i. | i | = 1 {\displaystyle |i|=1} |i|=1
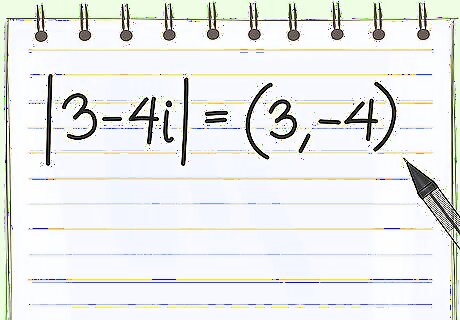
Find the coefficients of the complex equation. Think of 3-4i as an equation for a line. Absolute value is the distance from zero, so you want to find the distance from zero for the point (3, -4) on this line.The coefficients are simply the two numbers that aren't "i." While the number by the i is usually the second number, it doesn't actually matter when solving. To practice, find the following coefficients: | 1 + 6 i | {\displaystyle |1+6i|} |1+6i| = (1, 6) | 2 − i | {\displaystyle |2-i|} |2-i| = (2, -1) | 6 i − 8 | {\displaystyle |6i-8|} |6i-8| = (-8, 6)
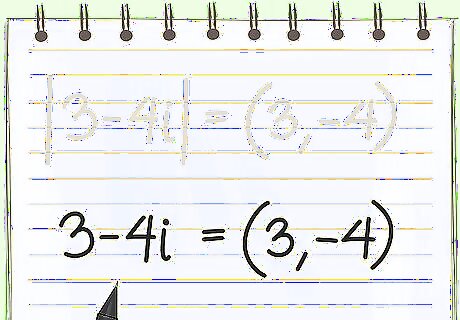
Remove the absolute value signs from the equation. All you need at this point are the coefficients. Remember, you need to find the distance from the equation to zero. Since you use the distance formula in the next step, this is the same thing as taking absolute value.
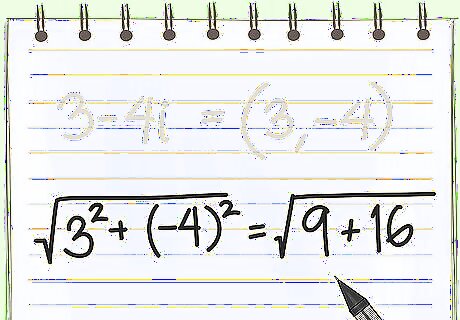
Square both coefficients. To find distance, you'll use the distance formula, known as x 2 + y 2 {\displaystyle {\sqrt {x^{2}+y^{2}}}} {\sqrt {x^{2}+y^{2}}}. So, for your first step, you need to square both coefficients of your complex equation. Continuing the example | 3 − 4 i | {\displaystyle |3-4i|} |3-4i|: Coefficients: (3, -4) Distance formula: 3 2 + ( − 4 ) 2 {\displaystyle {\sqrt {3^{2}+(-4)^{2}}}} {\sqrt {3^{2}+(-4)^{2}}} Square the coefficients: ' 9 + 16 {\displaystyle {\sqrt {9+16}}} {\sqrt {9+16}} Note: Review the distance formula if you're confused. Note now squaring both numbers makes them positive, effectively taking absolute value for you.

Add the squared numbers under the radical. The radical is the sign that takes the square root. Simply add them up, leaving the radical in place for now. Coefficients: (3, -4) Distance formula: 3 2 + ( − 4 ) 2 {\displaystyle {\sqrt {3^{2}+(-4)^{2}}}} {\sqrt {3^{2}+(-4)^{2}}} Square the coefficients: 9 + 16 {\displaystyle {\sqrt {9+16}}} {\sqrt {9+16}} Add up squared coefficients: 25 {\displaystyle {\sqrt {25}}} {\sqrt {25}}
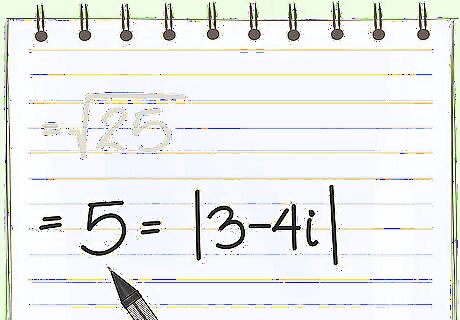
Take the square root to get your final answer. All you have to do is simplify the equation to get your final answer. This is the distance from your "point" on an imaginary graph zero. If there is no square root, just leave the answer from the last step under the radical-- this is a legitimate final answer. Coefficients: (3, -4) Distance formula: 3 2 + ( − 4 ) 2 {\displaystyle {\sqrt {3^{2}+(-4)^{2}}}} {\sqrt {3^{2}+(-4)^{2}}} Square the coefficients: 9 + 16 {\displaystyle {\sqrt {9+16}}} {\sqrt {9+16}} Add up squared coefficients: 25 {\displaystyle {\sqrt {25}}} {\sqrt {25}} Take the square root to get your final answer: 5 | 3 − 4 i | = 5 {\displaystyle |3-4i|=5} |3-4i|=5
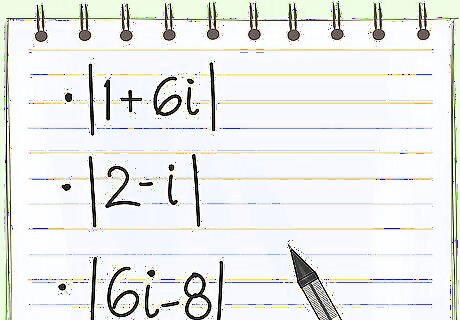
Try a few practice problems. Use your mouse to click and highlight right after the questions to see the answers, written here in white. | 1 + 6 i | {\displaystyle |1+6i|} |1+6i| = √37 | 2 − i | {\displaystyle |2-i|} |2-i| = √5 | 6 i − 8 | {\displaystyle |6i-8|} |6i-8| = 10


















Comments
0 comment